Formatted question description: https://leetcode.ca/all/2049.html

2049. Count Nodes With the Highest Score (Medium)

There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.

Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.

Return the number of nodes that have the highest score.

Example 1:

example-1

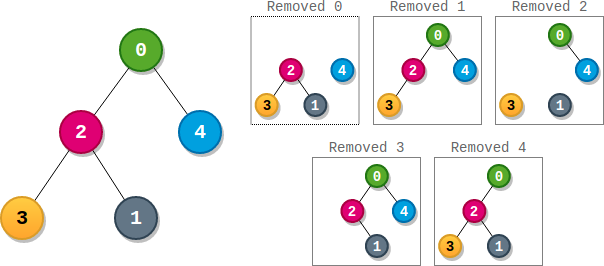
Input: parents = [-1,2,0,2,0]
Output: 3
Explanation:
- The score of node 0 is: 3 * 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 * 1 * 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.

Example 2:

example-2

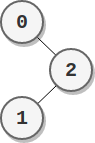
Input: parents = [-1,2,0]
Output: 2
Explanation:
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 * 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.

Constraints:

n == parents.length
2 <= n <= 10⁵
parents[0] == -1
0 <= parents[i] <= n - 1 for i != 0
parents represents a valid binary tree.

Similar Questions:

Solution 1. Post-order Traversal

Post-order traverse the tree. For each node, calculate its score by multiplying the node count of its left subtree, right subtree and nodes not in the current subtree (ignoring 0). Count the nodes with the maximum score.

// OJ: https://leetcode.com/problems/count-nodes-with-the-highest-score/
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int countHighestScoreNodes(vector<int>& P) {
        long N = P.size(), ans = 0, maxScore = 0;
        vector<vector<int>> G(N); // build the graph -- G[i] is a list of the children of node `i`.
        for (int i = 1; i < N; ++i) G[P[i]].push_back(i);
        function<int(int)> dfs = [&](int u) { // Post-order traversal. Returns the size of the subtree rooted at node `u`.
            long score = 1, cnt = 1;
            for (int v : G[u]) {
                int c = dfs(v);
                cnt += c;
                score *= c;
            }
            long other = N - cnt; // The count of nodes not in this subtree rooted at node `u`.
            if (other) score *= other;
            if (score > maxScore) {
                maxScore = score;
                ans = 1;
            } else if (score == maxScore) ++ans;
            return cnt;
        };
        dfs(0);
        return ans;
    }
};

class Solution:
    def countHighestScoreNodes(self, parents: List[int]) -> int:
        n, max_score, ans = len(parents), 0, 0
        g = [[] for _ in range(n)]
        for i in range(1, n):
            g[parents[i]].append(i)

        def dfs(cur: int) -> int:
            nonlocal max_score, ans
            size, score = 1, 1
            for c in g[cur]:
                s = dfs(c)
                size += s
                score *= s
            if cur > 0:
                score *= n - size
            if score > max_score:
                max_score = score
                ans = 1
            elif score == max_score:
                ans += 1
            return size

        dfs(0)
        return ans

############

# 2049. Count Nodes With the Highest Score
# https://leetcode.com/problems/count-nodes-with-the-highest-score

class Solution:
    def countHighestScoreNodes(self, parents: List[int]) -> int:
        nodes = collections.defaultdict(list)
        freq = collections.defaultdict(int)
        
        for i, x in enumerate(parents):
            if x >= 0:
                nodes[x].append(i)
        
        def go(x):
            left = right = 0
            
            if len(nodes[x]) >= 1:
                left = go(nodes[x][0])
            
            if len(nodes[x]) > 1:
                right = go(nodes[x][1])
            
            f = (left or 1) * (right or 1) * (len(parents) - 1 - left - right or 1)
            freq[f] += 1
            
            return 1 + left + right
        
        go(0)
        return freq[max(freq)]

class Solution {

    private int n;
    private long maxScore;
    private int ans;
    private List<List<Integer>> graph;

    public int countHighestScoreNodes(int[] parents) {
        n = parents.length;
        maxScore = 0;
        ans = 0;
        graph = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }
        for (int i = 1; i < n; i++) {
            graph.get(parents[i]).add(i);
        }
        dfs(0);
        return ans;
    }

    private int dfs(int cur) {
        int size = 1;
        long score = 1;
        for (int child : graph.get(cur)) {
            int s = dfs(child);
            size += s;
            score *= s;
        }
        if (cur > 0) {
            score *= n - size;
        }
        if (score > maxScore) {
            maxScore = score;
            ans = 1;
        } else if (score == maxScore) {
            ans++;
        }
        return size;
    }
}

func countHighestScoreNodes(parents []int) int {
	n := len(parents)
	g := make([][]int, n)
	for i := 1; i < n; i++ {
		p := parents[i]
		g[p] = append(g[p], i)
	}
	maxScore, ans := 0, 0
	var dfs func(int) int
	dfs = func(u int) int {
		size, score := 1, 1
		for _, v := range g[u] {
			t := dfs(v)
			size += t
			score *= t
		}
		if u > 0 {
			score *= n - size
		}
		if score > maxScore {
			maxScore, ans = score, 1
		} else if score == maxScore {
			ans++
		}
		return size
	}
	dfs(0)
	return ans
}

function countHighestScoreNodes(parents: number[]): number {
    const n = parents.length;
    let edge = Array.from({ length: n }, (v, i) => []);
    for (let i = 0; i < n; i++) {
        const parent = parents[i];
        if (parent != -1) {
            edge[parent].push(i);
        }
    }

    let ans = 0;
    let max = 0;
    function dfs(idx: number): number {
        let size = 1,
            score = 1;
        for (let i = 0; i < edge[idx].length; i++) {
            const child = edge[idx][i];
            let childSize = dfs(child);
            size += childSize;
            score *= childSize;
        }
        if (idx > 0) {
            score *= n - size;
        }
        if (score > max) {
            max = score;
            ans = 1;
        } else if (score == max) {
            ans++;
        }
        return size;
    }
    dfs(0);
    return ans;
}

public class Solution {
    private List<int>[] g;
    private int ans;
    private long mx;
    private int n;

    public int CountHighestScoreNodes(int[] parents) {
        n = parents.Length;
        g = new List<int>[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new List<int>();
        }
        for (int i = 1; i < n; ++i) {
            g[parents[i]].Add(i);
        }
        
        Dfs(0, -1);
        return ans;
    }

    private int Dfs(int i, int fa) {
        int cnt = 1;
        long score = 1;
        
        foreach (int j in g[i]) {
            if (j != fa) {
                int t = Dfs(j, i);
                cnt += t;
                score *= t;
            }
        }
        
        if (n - cnt > 0) {
            score *= n - cnt;
        }
        
        if (mx < score) {
            mx = score;
            ans = 1;
        } else if (mx == score) {
            ++ans;
        }
        
        return cnt;
    }
}

Discuss

https://leetcode.com/problems/count-nodes-with-the-highest-score/discuss/1537494/C%2B%2B-Post-order-Traversal

2049 - Count Nodes With the Highest Score

2049. Count Nodes With the Highest Score (Medium)

Solution 1. Post-order Traversal

Discuss

All Problems

All Solutions

Welcome to Subscribe On Youtube

2049. Count Nodes With the Highest Score (Medium)

Solution 1. Post-order Traversal

Discuss

All Problems

All Solutions