Welcome to Subscribe On Youtube

2133. Check if Every Row and Column Contains All Numbers

Description

An n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).

Given an n x n integer matrix matrix, return true if the matrix is valid. Otherwise, return false.

 

Example 1:

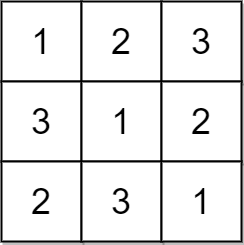
Input: matrix = [[1,2,3],[3,1,2],[2,3,1]]
Output: true
Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3.
Hence, we return true.

Example 2:

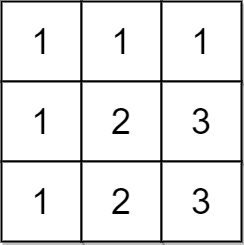
Input: matrix = [[1,1,1],[1,2,3],[1,2,3]]
Output: false
Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3.
Hence, we return false.

 

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• 1 <= matrix[i][j] <= n

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public boolean checkValid(int[][] matrix) {
          int n = matrix.length;
          for (int i = 0; i < n; ++i) {
              boolean[] seen = new boolean[n];
              for (int j = 0; j < n; ++j) {
                  int v = matrix[i][j] - 1;
                  if (seen[v]) {
                      return false;
                  }
                  seen[v] = true;
              }
          }
          for (int j = 0; j < n; ++j) {
              boolean[] seen = new boolean[n];
              for (int i = 0; i < n; ++i) {
                  int v = matrix[i][j] - 1;
                  if (seen[v]) {
                      return false;
                  }
                  seen[v] = true;
              }
          }
          return true;
      }
  }
  

• class Solution {
  public:
      bool checkValid(vector<vector<int>>& matrix) {
          int n = matrix.size();
          for (int i = 0; i < n; ++i) {
              vector<bool> seen(n);
              for (int j = 0; j < n; ++j) {
                  int v = matrix[i][j] - 1;
                  if (seen[v]) return false;
                  seen[v] = true;
              }
          }
          for (int j = 0; j < n; ++j) {
              vector<bool> seen(n);
              for (int i = 0; i < n; ++i) {
                  int v = matrix[i][j] - 1;
                  if (seen[v]) return false;
                  seen[v] = true;
              }
          }
          return true;
      }
  };
  

• class Solution:
      def checkValid(self, matrix: List[List[int]]) -> bool:
          n = len(matrix)
          for i in range(n):
              seen = [False] * n
              for j in range(n):
                  v = matrix[i][j] - 1
                  if seen[v]:
                      return False
                  seen[v] = True
          for j in range(n):
              seen = [False] * n
              for i in range(n):
                  v = matrix[i][j] - 1
                  if seen[v]:
                      return False
                  seen[v] = True
          return True
  
  

• func checkValid(matrix [][]int) bool {
  	n := len(matrix)
  	for i := 0; i < n; i++ {
  		seen := make([]bool, n)
  		for j := 0; j < n; j++ {
  			v := matrix[i][j] - 1
  			if seen[v] {
  				return false
  			}
  			seen[v] = true
  		}
  	}
  	for j := 0; j < n; j++ {
  		seen := make([]bool, n)
  		for i := 0; i < n; i++ {
  			v := matrix[i][j] - 1
  			if seen[v] {
  				return false
  			}
  			seen[v] = true
  		}
  	}
  	return true
  }
  

• function checkValid(matrix: number[][]): boolean {
      const n = matrix.length;
      let rows = Array.from({ length: n }, () => new Array(n).fill(false));
      let cols = Array.from({ length: n }, () => new Array(n).fill(false));
      for (let i = 0; i < n; i++) {
          for (let j = 0; j < n; j++) {
              let cur = matrix[i][j];
              if (rows[i][cur] || cols[j][cur]) return false;
              rows[i][cur] = true;
              cols[j][cur] = true;
          }
      }
      return true;
  }
  
  

All Problems

All Solutions