Formatted question description: https://leetcode.ca/all/1993.html

1993. Operations on Tree

Level

Medium

Description

You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of the i-th node. The root of the tree is node 0, so parent[0] = -1 since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.

The data structure should support the following functions:

Lock: Locks the given node for the given user and prevents other users from locking the same node. You may only lock a node if the node is unlocked.
Unlock: Unlocks the given node for the given user. You may only unlock a node if it is currently locked by the same user.
Upgrade: Locks the given node for the given user and unlocks all of its descendants. You may only upgrade a node if all 3 conditions are true:
- The node is unlocked,
- It has at least one locked descendant (by any user), and
- It does not have any locked ancestors.

Implement the LockingTree class:

LockingTree(int[] parent) initializes the data structure with the parent array.
lock(int num, int user) returns true if it is possible for the user with id user to lock the node num, or false otherwise. If it is possible, the node num will become locked by the user with id user.
unlock(int num, int user) returns true if it is possible for the user with id user to unlock the node num, or false otherwise. If it is possible, the node num will become unlocked.
upgrade(int num, int user) returns true if it is possible for the user with id user to upgrade the node num, or false otherwise. If it is possible, the node num will be upgraded.

Example 1:

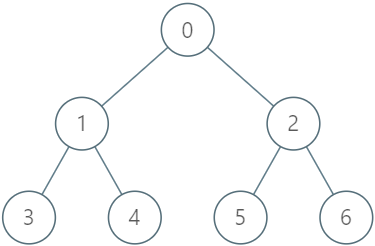
Image text

Input
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
Output
[null, true, false, true, true, true, false]

Explanation
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2);    // return true because node 2 is unlocked.
                           // Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3);  // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2);  // return true because node 2 was previously locked by user 2.
                           // Node 2 will now be unlocked.
lockingTree.lock(4, 5);    // return true because node 4 is unlocked.
                           // Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
                           // Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1);    // return false because node 0 is already locked.

Constraints:

n == parent.length
2 <= n <= 2000
0 <= parent[i] <= n - 1 for i != 0
parent[0] == -1
0 <= num <= n - 1
1 <= user <= 10^4
parent represents a valid tree.
At most 2000 calls in total will be made to lock, unlock, and upgrade.

Solution

In class LockingTree, store the number of nodes, the nodes’ parents, the nodes’ lock states, and the nodes’ children.

For the constructor, initialize the fields.

For lock, if the lock with num is unlocked, set it to locked with num and return true, otherwise return false.

For unlock, if the lock with num is locked with user, set it to unlocked and return true, otherwise return false.

For upgrade, check the conditions, and do the lock and unlock operations accordingly.

class LockingTree {
    int n;
    int[] parent;
    int[] locks;
    Set<Integer>[] children;

    public LockingTree(int[] parent) {
        n = parent.length;
        this.parent = parent;
        locks = new int[n];
        children = new Set[n];
        for (int i = 0; i < n; i++)
            children[i] = new HashSet<Integer>();
        for (int i = 1; i < n; i++) {
            int prev = parent[i];
            children[prev].add(i);
        }
    }
    
    public boolean lock(int num, int user) {
        if (locks[num] == 0) {
            locks[num] = user;
            return true;
        } else
            return false;
    }
    
    public boolean unlock(int num, int user) {
        if (locks[num] == user) {
            locks[num] = 0;
            return true;
        } else
            return false;
    }
    
    public boolean upgrade(int num, int user) {
        int node = num;
        while (node >= 0) {
            if (locks[node] != 0)
                return false;
            node = parent[node];
        }
        if (!breadthFirstSearch(num))
            return false;
        unlockAllDescendants(num);
        locks[num] = user;
        return true;
    }

    private boolean breadthFirstSearch(int num) {
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.offer(num);
        while (!queue.isEmpty()) {
            int node = queue.poll();
            if (locks[node] > 0)
                return true;
            Set<Integer> set = children[node];
            for (int next : set)
                queue.offer(next);
        }
        return false;
    }

    private void unlockAllDescendants(int num) {
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.offer(num);
        while (!queue.isEmpty()) {
            int node = queue.poll();
            locks[node] = 0;
            Set<Integer> set = children[node];
            for (int next : set)
                queue.offer(next);
        }
    }
}

/**
 * Your LockingTree object will be instantiated and called as such:
 * LockingTree obj = new LockingTree(parent);
 * boolean param_1 = obj.lock(num,user);
 * boolean param_2 = obj.unlock(num,user);
 * boolean param_3 = obj.upgrade(num,user);
 */

############

class LockingTree {
    private Map<Integer, Integer> nums;
    private int[] parent;
    private List<Integer>[] children;

    public LockingTree(int[] parent) {
        nums = new HashMap<>();
        this.parent = parent;
        int n = parent.length;
        children = new List[n];
        Arrays.setAll(children, k -> new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            if (parent[i] != -1) {
                children[parent[i]].add(i);
            }
        }
    }

    public boolean lock(int num, int user) {
        if (nums.containsKey(num)) {
            return false;
        }
        nums.put(num, user);
        return true;
    }

    public boolean unlock(int num, int user) {
        if (!nums.containsKey(num) || nums.get(num) != user) {
            return false;
        }
        nums.remove(num);
        return true;
    }

    public boolean upgrade(int num, int user) {
        int t = num;
        while (t != -1) {
            if (nums.containsKey(t)) {
                return false;
            }
            t = parent[t];
        }
        boolean[] find = new boolean[1];
        dfs(num, find);
        if (!find[0]) {
            return false;
        }
        nums.put(num, user);
        return true;
    }

    private void dfs(int num, boolean[] find) {
        for (int child : children[num]) {
            if (nums.containsKey(child)) {
                nums.remove(child);
                find[0] = true;
            }
            dfs(child, find);
        }
    }
}

/**
 * Your LockingTree object will be instantiated and called as such:
 * LockingTree obj = new LockingTree(parent);
 * boolean param_1 = obj.lock(num,user);
 * boolean param_2 = obj.unlock(num,user);
 * boolean param_3 = obj.upgrade(num,user);
 */

// OJ: https://leetcode.com/problems/operations-on-tree/
// Time:
//      LockingTree: O(N)
//      lock: O(1)
//      unlock: O(1)
//      upgrade: O(N)
// Space: O(N)
class LockingTree {
    vector<int> locked, parent;
    vector<vector<int>> child;
    int N;
    bool upwardValid(int i) {
        if (i == -1) return true;
        if (locked[i]) return false;
        return upwardValid(parent[i]);
    }
    bool downwardValid(int i) {
        if (locked[i]) return true;
        for (int ch : child[i]) {
            if (downwardValid(ch)) return true;
        }
        return false;
    }
    void downwardUnlock(int i) {
        locked[i] = 0;
        for (int ch : child[i]) {
            downwardUnlock(ch);
        }
    }
public:
    LockingTree(vector<int>& parent) : parent(parent) {
        N = parent.size();
        locked.assign(N, 0);
        child.assign(N, vector<int>());
        for (int i = 1; i < N; ++i) {
            child[parent[i]].push_back(i);
        }
    }
    
    bool lock(int num, int user) {
        if (locked[num] != 0) return false;
        locked[num] = user;
        return true;
    }
    
    bool unlock(int num, int user) {
        if (locked[num] != user) return false;
        locked[num] = 0;
        return true;
    }
    
    bool upgrade(int num, int user) {
        if (!upwardValid(num) || !downwardValid(num)) return false;
        downwardUnlock(num);
        locked[num] = user;
        return true;
    }
};

class LockingTree:
    def __init__(self, parent: List[int]):
        self.nums = {}
        self.parent = parent
        self.children = defaultdict(list)
        for i, p in enumerate(parent):
            self.children[p].append(i)

    def lock(self, num: int, user: int) -> bool:
        if num in self.nums:
            return False
        self.nums[num] = user
        return True

    def unlock(self, num: int, user: int) -> bool:
        if num not in self.nums or self.nums[num] != user:
            return False
        self.nums.pop(num)
        return True

    def upgrade(self, num: int, user: int) -> bool:
        def dfs(num):
            nonlocal find
            for child in self.children[num]:
                if child in self.nums:
                    self.nums.pop(child)
                    find = True
                dfs(child)

        t = num
        while t != -1:
            if t in self.nums:
                return False
            t = self.parent[t]
        find = False
        dfs(num)
        if not find:
            return False
        self.nums[num] = user
        return True


# Your LockingTree object will be instantiated and called as such:
# obj = LockingTree(parent)
# param_1 = obj.lock(num,user)
# param_2 = obj.unlock(num,user)
# param_3 = obj.upgrade(num,user)

############

# 1993. Operations on Tree
# https://leetcode.com/problems/operations-on-tree

class LockingTree:

    def __init__(self, parent: List[int]):
        self.parent = parent
        self.locked = [None] * len(parent)
        self.child = collections.defaultdict(list)
        
        for i in range(1, len(parent)):
            self.child[parent[i]].append(i)

    def lock(self, num: int, user: int) -> bool:
        if self.locked[num]: return False
        self.locked[num] = user
        return True

    def unlock(self, num: int, user: int) -> bool:
        if self.locked[num] != user: return False
        self.locked[num] = None
        return True

    def upgrade(self, num: int, user: int) -> bool:
        i = num
        while i != -1:
            if self.locked[i]: return False
            i = self.parent[i]
        
        count, queue = 0, collections.deque([num])
        while queue:
            n = queue.popleft()
            if self.locked[n]:
                self.locked[n] = None
                count += 1
            
            queue.extend(self.child[n])
        
        if count > 0:
            self.locked[num] = user
        
        return count > 0
            


# Your LockingTree object will be instantiated and called as such:
# obj = LockingTree(parent)
# param_1 = obj.lock(num,user)
# param_2 = obj.unlock(num,user)
# param_3 = obj.upgrade(num,user)

type LockingTree struct {
	nums     map[int]int
	parent   []int
	children [][]int
}

func Constructor(parent []int) LockingTree {
	n := len(parent)
	nums := make(map[int]int)
	children := make([][]int, n)
	for i, p := range parent {
		if p != -1 {
			children[p] = append(children[p], i)
		}
	}
	return LockingTree{nums, parent, children}
}

func (this *LockingTree) Lock(num int, user int) bool {
	if _, ok := this.nums[num]; ok {
		return false
	}
	this.nums[num] = user
	return true
}

func (this *LockingTree) Unlock(num int, user int) bool {
	if this.nums[num] != user {
		return false
	}
	delete(this.nums, num)
	return true
}

func (this *LockingTree) Upgrade(num int, user int) bool {
	for t := num; t != -1; t = this.parent[t] {
		if _, ok := this.nums[t]; ok {
			return false
		}
	}
	find := false
	var dfs func(int)
	dfs = func(num int) {
		for _, child := range this.children[num] {
			if _, ok := this.nums[child]; ok {
				delete(this.nums, child)
				find = true
			}
			dfs(child)
		}
	}
	dfs(num)
	if !find {
		return false
	}
	this.nums[num] = user
	return true
}

/**
 * Your LockingTree object will be instantiated and called as such:
 * obj := Constructor(parent);
 * param_1 := obj.Lock(num,user);
 * param_2 := obj.Unlock(num,user);
 * param_3 := obj.Upgrade(num,user);
 */

class LockingTree {
    private locked: number[];
    private parent: number[];
    private children: number[][];

    constructor(parent: number[]) {
        const n = parent.length;
        this.locked = Array(n).fill(-1);
        this.parent = parent;
        this.children = Array(n)
            .fill(0)
            .map(() => []);
        for (let i = 1; i < n; i++) {
            this.children[parent[i]].push(i);
        }
    }

    lock(num: number, user: number): boolean {
        if (this.locked[num] === -1) {
            this.locked[num] = user;
            return true;
        }
        return false;
    }

    unlock(num: number, user: number): boolean {
        if (this.locked[num] === user) {
            this.locked[num] = -1;
            return true;
        }
        return false;
    }

    upgrade(num: number, user: number): boolean {
        let x = num;
        for (; x !== -1; x = this.parent[x]) {
            if (this.locked[x] !== -1) {
                return false;
            }
        }
        let find = false;
        const dfs = (x: number) => {
            for (const y of this.children[x]) {
                if (this.locked[y] !== -1) {
                    this.locked[y] = -1;
                    find = true;
                }
                dfs(y);
            }
        };
        dfs(num);
        if (!find) {
            return false;
        }
        this.locked[num] = user;
        return true;
    }
}

/**
 * Your LockingTree object will be instantiated and called as such:
 * var obj = new LockingTree(parent)
 * var param_1 = obj.lock(num,user)
 * var param_2 = obj.unlock(num,user)
 * var param_3 = obj.upgrade(num,user)
 */

1993 - Operations on Tree

1993. Operations on Tree

Level

Description

Solution

All Problems

All Solutions

Welcome to Subscribe On Youtube

1993. Operations on Tree

Level

Description

Solution

All Problems

All Solutions