Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1981.html

1981. Minimize the Difference Between Target and Chosen Elements

Level

Medium

Description

You are given an m x n integer matrix mat and an integer target.

Choose one integer from each row in the matrix such that the absolute difference between target and the sum of the chosen elements is minimized.

Return the minimum absolute difference.

The absolute difference between two numbers a and b is the absolute value of a - b.

Example 1:

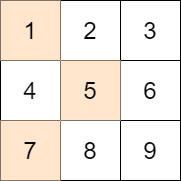
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13

Output: 0

*Explanation:8 One possible choice is to:

• Choose 1 from the first row.
• Choose 5 from the second row.
• Choose 7 from the third row.

The sum of the chosen elements is 13, which equals the target, so the absolute difference is 0.

Example 2:

Input: mat = [[1],[2],[3]], target = 100

Output: 94

Explanation: The best possible choice is to:

• Choose 1 from the first row.
• Choose 2 from the second row.
• Choose 3 from the third row.

The sum of the chosen elements is 6, and the absolute difference is 94.

Example 3:

Input: mat = [[1,2,9,8,7]], target = 6

Output: 1

Explanation: The best choice is to choose 7 from the first row.

The absolute difference is 1.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 70
• 1 <= mat[i][j] <= 70
• 1 <= target <= 800

Solution

Use dynamic programming. Create a 2D array dp with m + 1 rows and 4901 columns, where dp[i][j] represents whether sum j is reachable by using the first i rows of mat. Loop over mat to fill in the values in dp. Finally, loop over the last row of dp and find the value j such that dp[m][j] = true and j is closest to target. Return the absolute difference between j and target.

• Java
• C++
• Python
• Go

• class Solution {
      public int minimizeTheDifference(int[][] mat, int target) {
          int rows = mat.length, columns = mat[0].length;
          boolean[][] dp = new boolean[rows + 1][4901];
          dp[0][0] = true;
          for (int i = 0; i < rows; i++) {
              for (int j = 0; j <= 4900; j++) {
                  if (dp[i][j]) {
                      for (int k = 0; k < columns; k++)
                          dp[i + 1][j + mat[i][k]] = true;
                  }
              }
          }
          int minDifference = Integer.MAX_VALUE;
          for (int j = 0; j <= 4900; j++) {
              if (dp[rows][j]) {
                  int difference = Math.abs(j - target);
                  minDifference = Math.min(minDifference, difference);
              }
          }
          return minDifference;
      }
  }
  
  ############
  
  class Solution {
      public int minimizeTheDifference(int[][] mat, int target) {
          boolean[] f = {true};
          for (var row : mat) {
              int mx = 0;
              for (int x : row) {
                  mx = Math.max(mx, x);
              }
              boolean[] g = new boolean[f.length + mx];
              for (int x : row) {
                  for (int j = x; j < f.length + x; ++j) {
                      g[j] |= f[j - x];
                  }
              }
              f = g;
          }
          int ans = 1 << 30;
          for (int j = 0; j < f.length; ++j) {
              if (f[j]) {
                  ans = Math.min(ans, Math.abs(j - target));
              }
          }
          return ans;
      }
  }
  

• // OJ: https://leetcode.com/problems/minimize-the-difference-between-target-and-chosen-elements/
  // Time: O(M^2 * KN)
  // Space: O(MK)
  const int maxN = 4901; 
  class Solution {
  public:
      int minimizeTheDifference(vector<vector<int>>& A, int target) {
          int M = A.size(), N = A[0].size(), minSum = 0, maxSum = 0;
          bitset<maxN> bs(1);
          for (auto &v : A) {
              bitset<maxN> next;
              int mx = 0, mn = INT_MAX;
              sort(begin(v), end(v));
              for (int i = 0; i < N; ++i) {
                  while (i + 1 < N && v[i + 1] == v[i]) ++i;
                  next |= bs << v[i];
                  mx = max(mx, v[i]);
                  mn = min(mn, v[i]);
              }
              maxSum += mx;
              minSum += mn;
              swap(next, bs);
          }
          int i = target, ans = INT_MAX;
          for (; i >= minSum && !bs[i]; --i);
          if (i >= minSum) ans = target - i;
          for (i = target; i <= maxSum && !bs[i]; ++i);
          if (i <= maxSum) ans = min(ans, i - target);
          return ans;
      }
  };
  

• class Solution:
      def minimizeTheDifference(self, mat: List[List[int]], target: int) -> int:
          f = {0}
          for row in mat:
              f = set(a + b for a in f for b in row)
          return min(abs(v - target) for v in f)
  
  ############
  
  # 1981. Minimize the Difference Between Target and Chosen Elements
  # https://leetcode.com/problems/minimize-the-difference-between-target-and-chosen-elements/
  
  class Solution:
      def minimizeTheDifference(self, mat: List[List[int]], target: int) -> int:
          nums = {0}
          
          for row in mat:
              nums = {num + x for x in row for num in nums}
          
          return min(abs(x - target) for x in nums)
  
  

• func minimizeTheDifference(mat [][]int, target int) int {
  	f := []int{1}
  	for _, row := range mat {
  		mx := 0
  		for _, x := range row {
  			mx = max(mx, x)
  		}
  		g := make([]int, len(f)+mx)
  		for _, x := range row {
  			for j := x; j < len(f)+x; j++ {
  				g[j] |= f[j-x]
  			}
  		}
  		f = g
  	}
  	ans := 1 << 30
  	for j, v := range f {
  		if v == 1 {
  			ans = min(ans, abs(j-target))
  		}
  	}
  	return ans
  }
  
  func max(a, b int) int {
  	if a > b {
  		return a
  	}
  	return b
  }
  
  func min(a, b int) int {
  	if a < b {
  		return a
  	}
  	return b
  }
  
  func abs(x int) int {
  	if x < 0 {
  		return -x
  	}
  	return x
  }
  

All Problems

All Solutions