Welcome to Subscribe On Youtube
2093. Minimum Cost to Reach City With Discounts
Description
A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.
Return the minimum total cost to go from city 0 to city n - 1, or -1 if it is not possible to go from city 0 to city n - 1.
Example 1:
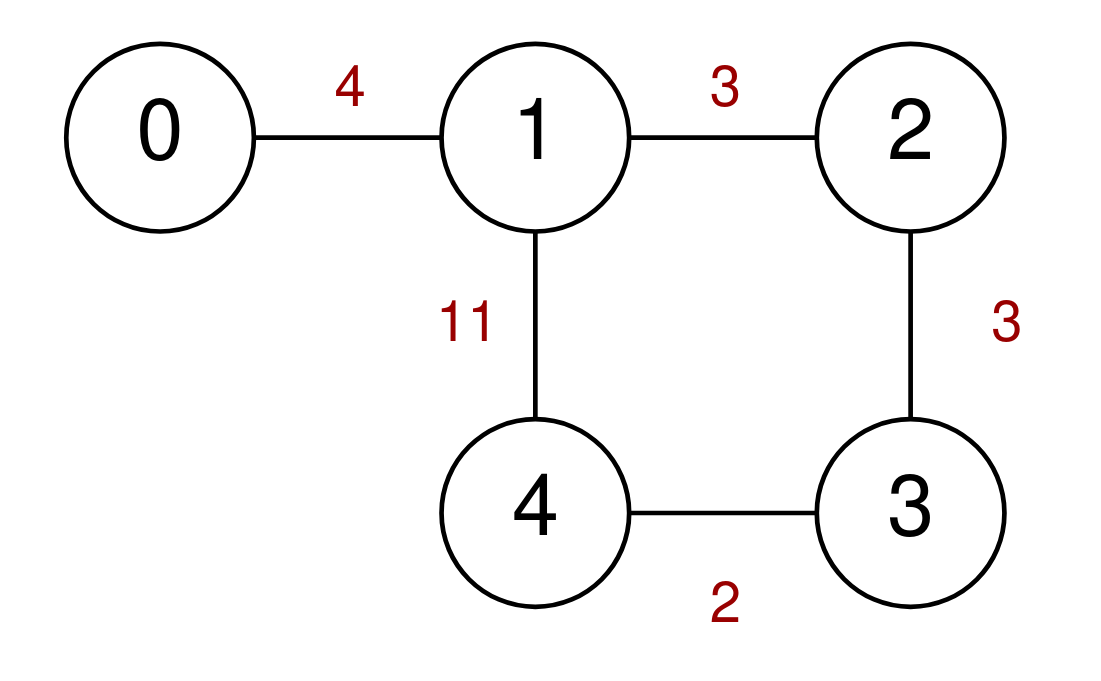
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1 Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
Example 2:
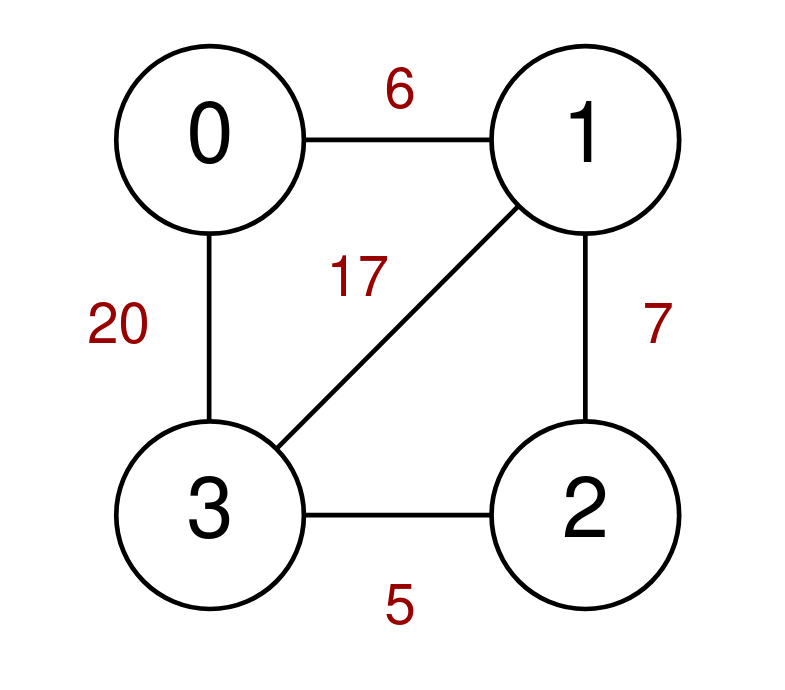
Input: n = 4, highways = [[1,3,17],[1,2,7],[3,2,5],[0,1,6],[3,0,20]], discounts = 20 Output: 8 Explanation: Go from 0 to 1 and use a discount for a cost of 6 / 2 = 3. Go from 1 to 2 and use a discount for a cost of 7 / 2 = 3. Go from 2 to 3 and use a discount for a cost of 5 / 2 = 2. The minimum cost to go from 0 to 3 is 3 + 3 + 2 = 8.
Example 3:

Input: n = 4, highways = [[0,1,3],[2,3,2]], discounts = 0 Output: -1 Explanation: It is impossible to go from 0 to 3 so return -1.
Constraints:
2 <= n <= 10001 <= highways.length <= 1000highways[i].length == 30 <= city1i, city2i <= n - 1city1i != city2i0 <= tolli <= 1050 <= discounts <= 500- There are no duplicate highways.
Solutions
-
class Solution { public int minimumCost(int n, int[][] highways, int discounts) { List<int[]>[] g = new List[n]; for (int i = 0; i < n; ++i) { g[i] = new ArrayList<>(); } for (var e : highways) { int a = e[0], b = e[1], c = e[2]; g[a].add(new int[] {b, c}); g[b].add(new int[] {a, c}); } PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]); q.offer(new int[] {0, 0, 0}); int[][] dist = new int[n][discounts + 1]; for (var e : dist) { Arrays.fill(e, Integer.MAX_VALUE); } while (!q.isEmpty()) { var p = q.poll(); int cost = p[0], i = p[1], k = p[2]; if (k > discounts || dist[i][k] <= cost) { continue; } if (i == n - 1) { return cost; } dist[i][k] = cost; for (int[] nxt : g[i]) { int j = nxt[0], v = nxt[1]; q.offer(new int[] {cost + v, j, k}); q.offer(new int[] {cost + v / 2, j, k + 1}); } } return -1; } } -
class Solution { public: int minimumCost(int n, vector<vector<int>>& highways, int discounts) { vector<vector<pair<int, int>>> g(n); for (auto& e : highways) { int a = e[0], b = e[1], c = e[2]; g[a].push_back({b, c}); g[b].push_back({a, c}); } priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> q; q.push({0, 0, 0}); vector<vector<int>> dist(n, vector<int>(discounts + 1, INT_MAX)); while (!q.empty()) { auto [cost, i, k] = q.top(); q.pop(); if (k > discounts || dist[i][k] <= cost) continue; if (i == n - 1) return cost; dist[i][k] = cost; for (auto [j, v] : g[i]) { q.push({cost + v, j, k}); q.push({cost + v / 2, j, k + 1}); } } return -1; } }; -
class Solution: def minimumCost(self, n: int, highways: List[List[int]], discounts: int) -> int: g = defaultdict(list) for a, b, c in highways: g[a].append((b, c)) g[b].append((a, c)) q = [(0, 0, 0)] dist = [[inf] * (discounts + 1) for _ in range(n)] while q: cost, i, k = heappop(q) if k > discounts: continue if i == n - 1: return cost if dist[i][k] > cost: dist[i][k] = cost for j, v in g[i]: heappush(q, (cost + v, j, k)) heappush(q, (cost + v // 2, j, k + 1)) return -1