Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1973.html

1973. Count Nodes Equal to Sum of Descendants

Level

Medium

Description

Given the root of a binary tree, return the number of nodes where the value of the node is equal to the sum of the values of its descendants.

A descendant of a node x is any node that is on the path from node x to some leaf node. The sum is considered to be 0 if the node has no descendants.

Example 1:

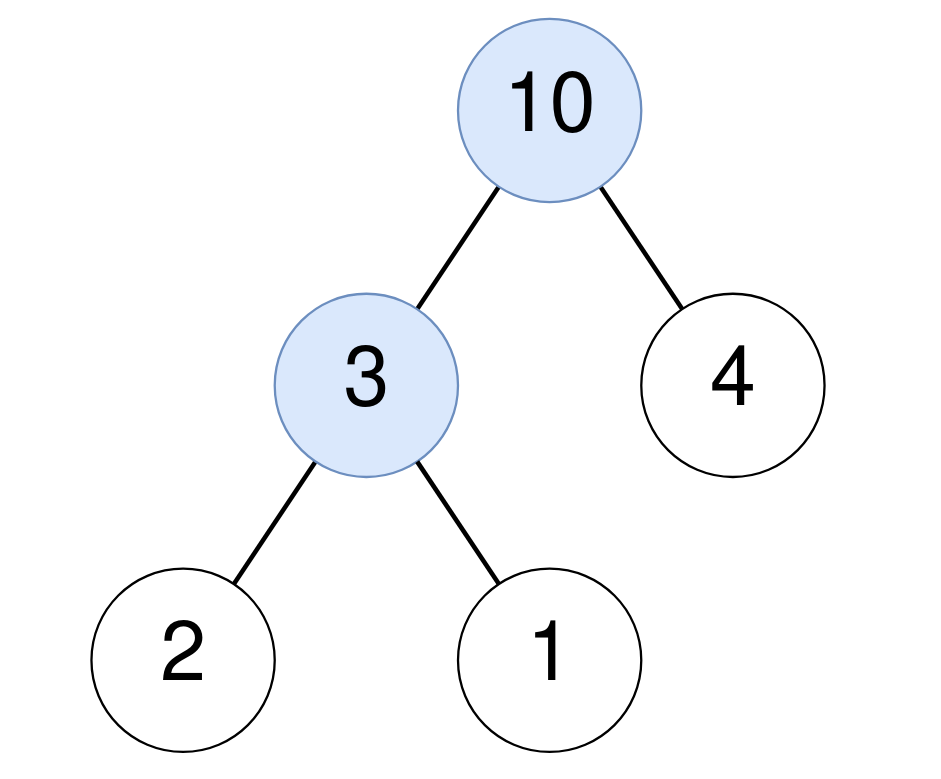
Input: root = [10,3,4,2,1]

Output: 2

Explanation:

For the node with value 10: The sum of its descendants is 3+4+2+1 = 10.

For the node with value 3: The sum of its descendants is 2+1 = 3.

Example 2:

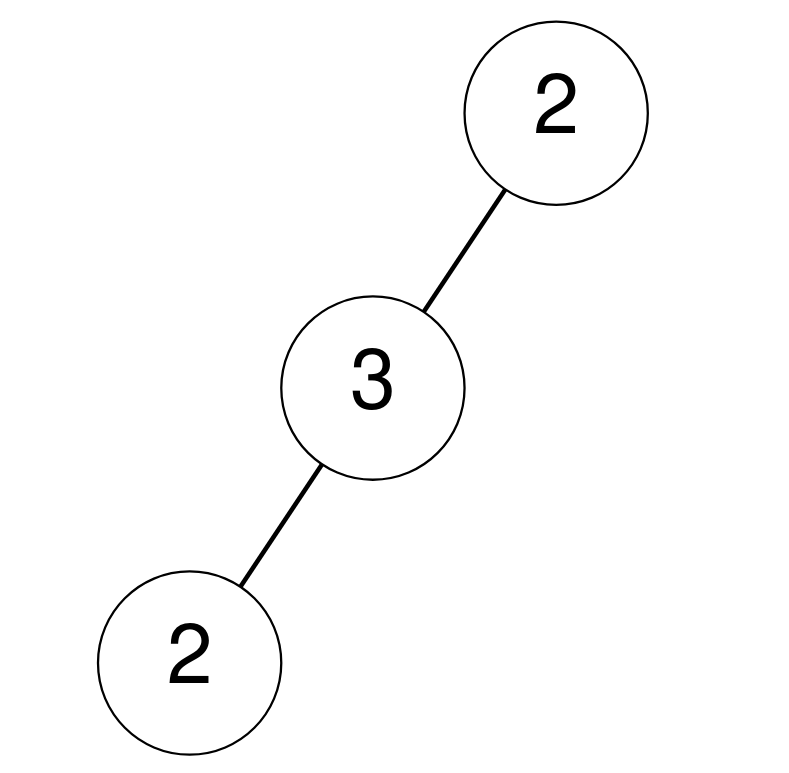
Input: root = [2,3,null,2,null]

Output: 0

Explanation:

No node has a value that is equal to the sum of its descendants.

Example 3:

Input: root = [0]

Output: 1

For the node with value 0: The sum of its descendants is 0 since it has no descendants.

Constraints:

• The number of nodes in the tree is in the range [1, 10^5].
• 0 <= Node.val <= 10^5

Solution

Do depth first search on the binary tree. For each node, calculate the sum of descedants and check whether the sum of descedants is equal to the node’s value. If so, add the counter by 1. Finally, return the counter.

• Java
• C++
• Python
• Go

• /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      int count = 0;
  
      public int equalToDescendants(TreeNode root) {
          getSum(root);
          return count;
      }
  
      public int getSum(TreeNode root) {
          if (root == null)
              return 0;
          int childrenSum = getSum(root.left) + getSum(root.right);
          if (childrenSum == root.val)
              count++;
          return childrenSum + root.val;
      }
  }
  
  ############
  
  /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      private int ans;
  
      public int equalToDescendants(TreeNode root) {
          dfs(root);
          return ans;
      }
  
      private int dfs(TreeNode root) {
          if (root == null) {
              return 0;
          }
          int l = dfs(root.left);
          int r = dfs(root.right);
          if (l + r == root.val) {
              ++ans;
          }
          return root.val + l + r;
      }
  }
  

• // OJ: https://leetcode.com/problems/count-nodes-equal-to-sum-of-descendants/
  // Time: O(N)
  // Space: O(H)
  class Solution {
      int ans = 0;
      long dfs(TreeNode *root) {
          if (!root) return 0; 
          long sum = dfs(root->left) + dfs(root->right);
          if (root->val == sum) ++ans;
          return sum + root->val;
      }
  public:
      int equalToDescendants(TreeNode* root) {
          dfs(root);
          return ans;
      }
  };
  

• # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right
  class Solution:
      def equalToDescendants(self, root: Optional[TreeNode]) -> int:
          def dfs(root):
              if root is None:
                  return 0
              l, r = dfs(root.left), dfs(root.right)
              if l + r == root.val:
                  nonlocal ans
                  ans += 1
              return root.val + l + r
  
          ans = 0
          dfs(root)
          return ans
  
  

• /**
   * Definition for a binary tree node.
   * type TreeNode struct {
   *     Val int
   *     Left *TreeNode
   *     Right *TreeNode
   * }
   */
  func equalToDescendants(root *TreeNode) (ans int) {
  	var dfs func(*TreeNode) int
  	dfs = func(root *TreeNode) int {
  		if root == nil {
  			return 0
  		}
  		l, r := dfs(root.Left), dfs(root.Right)
  		if l+r == root.Val {
  			ans++
  		}
  		return root.Val + l + r
  	}
  	dfs(root)
  	return
  }
  

All Problems

All Solutions