Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1954.html
1954. Minimum Garden Perimeter to Collect Enough Apples
Level
Medium
Description
In a garden represented as an infinite 2D grid, there is an apple tree planted at every integer coordinate. The apple tree planted at an integer coordinate (i, j) has |i| + |j| apples growing on it.
You will buy an axis-aligned square plot of land that is centered at (0, 0).
Given an integer neededApples, return the minimum perimeter of a plot such that at least neededApples apples are inside or on the perimeter of that plot.
The value of |x| is defined as:
xifx >= 0-xifx < 0
Example 1:
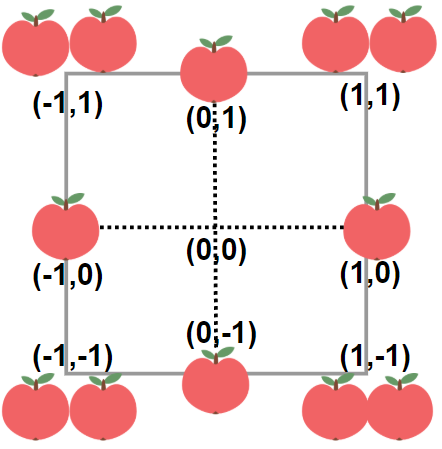
Input: neededApples = 1
Output: 8
Explanation: A square plot of side length 1 does not contain any apples.
However, a square plot of side length 2 has 12 apples inside (as depicted in the image above).
The perimeter is 2 * 4 = 8.
Example 2:
Input: neededApples = 13
Output: 16
Example 3:
Input: neededApples = 1000000000
Output: 5040
Constraints:
1 <= neededApples <= 10^15
Solution
Obviously, the side of the garden must be even. Once the side of the garden is determined, the number of apples in the garden can be calculated. Use binary search to find the minimum garden side to collect enough apples. The perimeter is the garden side multipled by 4.
-
class Solution { public long minimumPerimeter(long neededApples) { long low = 2, high = Math.min(neededApples, 1000000); if (high % 2 == 1) high--; while (low < high) { long mid = (high - low) / 2 + low; if (mid % 2 == 1) mid--; long apples = countApples(mid); if (apples < neededApples) low = mid + 2; else high = mid; } return low * 4; } public long countApples(long side) { long center = side / 2 * (side / 2 + 1); long start = center + side + 1; long end = center + (side + 1) * side / 2; long total = (start + end) * side / 2 + center; return total; } } -
// OJ: https://leetcode.com/problems/minimum-garden-perimeter-to-collect-enough-apples/ // Time: O(root(T, 3)) // Space: O(1) class Solution { public: long long minimumPerimeter(long long target) { long long sum = 0, f = 0, i = 1; for (; true; ++i) { f += i * (i + 1) * 3 / 2; sum = f * 8 - 6 * i * (i + 1); if (sum >= target) return 8 * i; } } }; -
# 1954. Minimum Garden Perimeter to Collect Enough Apples # https://leetcode.com/problems/minimum-garden-perimeter-to-collect-enough-apples class Solution: def minimumPerimeter(self, neededApples: int) -> int: i = 1 curr = 0 while True: first = i + 1 last = (i * 2) - 1 temp = ((first + last) * (last - first + 1)) // 2 temp *= 8 temp += (i * 4) + (i * 2) * 4 curr += temp if curr >= neededApples: break i += 1 return i * 8 -
func minimumPerimeter(neededApples int64) int64 { var l, r int64 = 1, 100000 for l < r { mid := (l + r) >> 1 if 2*mid*(mid+1)*(2*mid+1) >= neededApples { r = mid } else { l = mid + 1 } } return l * 8 } -
function minimumPerimeter(neededApples: number): number { let l = 1; let r = 100000; while (l < r) { const mid = (l + r) >> 1; if (2 * mid * (mid + 1) * (2 * mid + 1) >= neededApples) { r = mid; } else { l = mid + 1; } } return 8 * l; }