Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1943.html
1943. Describe the Painting
Level
Medium
Description
There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a unique color. You are given a 2D integer array segments, where segments[i] = [start_i, end_i, color_i] represents the half-closed segment [start_i, end_i) with color_i as the color.
The colors in the overlapping segments of the painting were mixed when it was painted. When two or more colors mix, they form a new color that can be represented as a set of mixed colors.
- For example, if colors
2,4, and6are mixed, then the resulting mixed color is{2,4,6}.
For the sake of simplicity, you should only output the sum of the elements in the set rather than the full set.
You want to describe the painting with the minimum number of non-overlapping half-closed segments of these mixed colors. These segments can be represented by the 2D array painting where painting[j] = [left_j, right_j, mix_j] describes a half-closed segment [left_j, right_j) with the mixed color sum of mix_j.
- For example, the painting created with
segments = [[1,4,5],[1,7,7]]can be described bypainting = [[1,4,12],[4,7,7]]because:[1,4)is colored{5,7}(with a sum of12) from both the first and second segments.[4,7)is colored{7}from only the second segment.
Return the 2D array painting describing the finished painting (excluding any parts that are not painted). You may return the segments in any order.
A half-closed segment [a, b) is the section of the number line between points a and b including point a and not including point b.
Example 1:
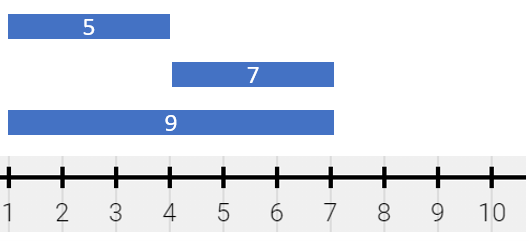
Input: segments = [[1,4,5],[4,7,7],[1,7,9]]
Output: [[1,4,14],[4,7,16]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- [4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
Example 2:
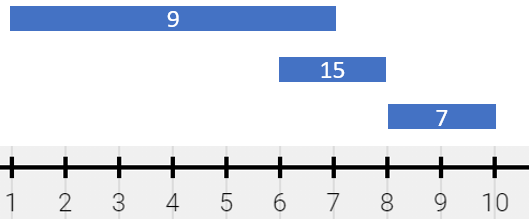
Input: segments = [[1,7,9],[6,8,15],[8,10,7]]
Output: [[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
Explanation: The painting can be described as follows:
- [1,6) is colored 9 from the first segment.
- [6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- [7,8) is colored 15 from the second segment.
- [8,10) is colored 7 from the third segment.
Example 3:
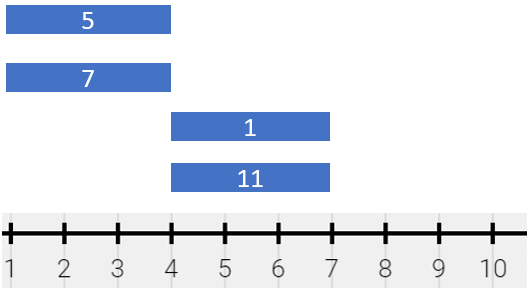
Input: segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
Output: [[1,4,12],[4,7,12]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- [4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment [1,7) is incorrect because the mixed color sets are different.
Constraints:
1 <= segments.length <= 2 * 10^4segments[i].length == 31 <= start_i < end_i <= 10^51 <= colori <= 10^9- Each
color_iis distinct.
Solution
Use the idea of prefix sum. For each segment, if the color is color, add color to the start of the segment and add -color to the end of the segment. After looping over all segments, the final segments are determined. Calculate each segment’s sum of colors and return the segments.
-
class Solution { public List<List<Long>> splitPainting(int[][] segments) { Map<Integer, Long> map = new HashMap<Integer, Long>(); int length = segments.length; map.put(segments[0][0], (long) segments[0][2]); map.put(segments[0][1], (long) (-segments[0][2])); for (int i = 1; i < length; i++) { int[] segment = segments[i]; int start = segment[0], end = segment[1]; long color = segment[2]; map.put(start, map.getOrDefault(start, 0L) + color); map.put(end, map.getOrDefault(end, 0L) - color); } List<List<Long>> paintings = new ArrayList<List<Long>>(); List<Integer> keyList = new ArrayList<Integer>(map.keySet()); Collections.sort(keyList); long currColor = 0; int size = keyList.size(); for (int i = 1; i < size; i++) { int start = keyList.get(i - 1), end = keyList.get(i); long colorDiff = map.get(start); currColor += colorDiff; if (currColor != 0) paintings.add(Arrays.asList((long) start, (long) end, currColor)); } return paintings; } } ############ class Solution { public List<List<Long>> splitPainting(int[][] segments) { TreeMap<Integer, Long> d = new TreeMap<>(); for (int[] e : segments) { int l = e[0], r = e[1], c = e[2]; d.put(l, d.getOrDefault(l, 0L) + c); d.put(r, d.getOrDefault(r, 0L) - c); } List<List<Long>> ans = new ArrayList<>(); long i = 0, j = 0; long cur = 0; for (Map.Entry<Integer, Long> e : d.entrySet()) { if (Objects.equals(e.getKey(), d.firstKey())) { i = e.getKey(); } else { j = e.getKey(); if (cur > 0) { ans.add(Arrays.asList(i, j, cur)); } i = j; } cur += e.getValue(); } return ans; } } -
// OJ: https://leetcode.com/problems/describe-the-painting/ // Time: O(N + M) where M is maximum end time. // Space: O(M) class Solution { public: vector<vector<long long>> splitPainting(vector<vector<int>>& A) { long long sum[100001] = {}; bool change[100001] = {}; int last = 0; for (auto &a : A) { int s = a[0], e = a[1], c = a[2]; sum[s] += c; sum[e] -= c; change[s] = change[e] = true; last = max(last, e); } for (int i = 1; i <= last; ++i) { sum[i] += sum[i - 1]; } vector<vector<long long>> ans; for (int i = 0; i <= last; ) { int start = i; while (i <= last && sum[i] == sum[start] && (i == start || !change[i])) ++i; if (sum[start]) { ans.push_back({ start, i, sum[start] }); } } return ans; } }; -
class Solution: def splitPainting(self, segments: List[List[int]]) -> List[List[int]]: d = defaultdict(int) for l, r, c in segments: d[l] += c d[r] -= c s = sorted([[k, v] for k, v in d.items()]) n = len(s) for i in range(1, n): s[i][1] += s[i - 1][1] return [[s[i][0], s[i + 1][0], s[i][1]] for i in range(n - 1) if s[i][1]] ############ # 1943. Describe the Painting # https://leetcode.com/problems/describe-the-painting/ class Solution: def splitPainting(self, segments: List[List[int]]) -> List[List[int]]: painting = [0] * (10 ** 5 + 1) ends = set() for start, end, color in segments: painting[start] += color painting[end] -= color ends.add(end) for i in range(1, 10 ** 5 + 1): painting[i] += painting[i - 1] res = [] currentStart = -1 currentColor = 0 for i, x in enumerate(painting): if currentStart == -1 and x > 0: currentStart = i currentColor = x continue if i in ends or currentColor != x: if currentColor > 0: res.append([currentStart, i, currentColor]) currentStart = i currentColor = x return res