Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1937.html
1937. Maximum Number of Points with Cost
Level
Medium
Description
You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.
To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.
Return the maximum number of points you can achieve.
abs(x) is defined as:
xforx >= 0.-xforx < 0.
Example 1:
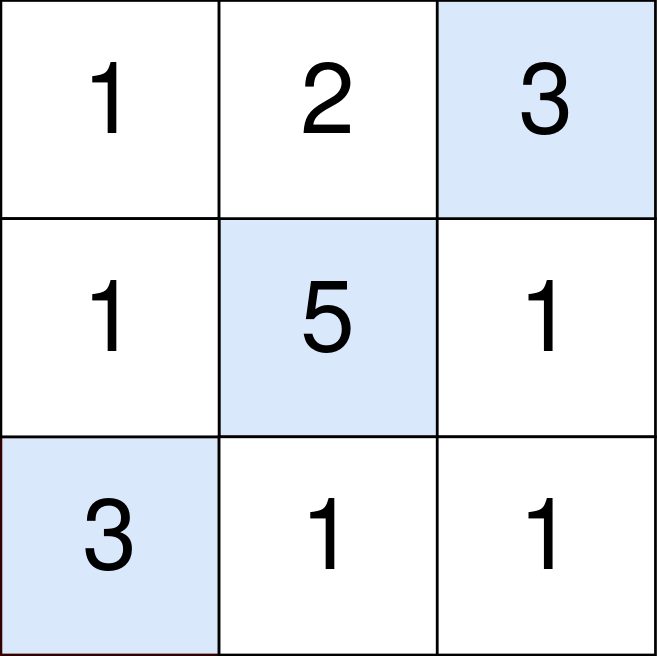
Input: points = [[1,2,3],[1,5,1],[3,1,1]]
Output: 9
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score. Your final score is 11 - 2 = 9.
Example 2:
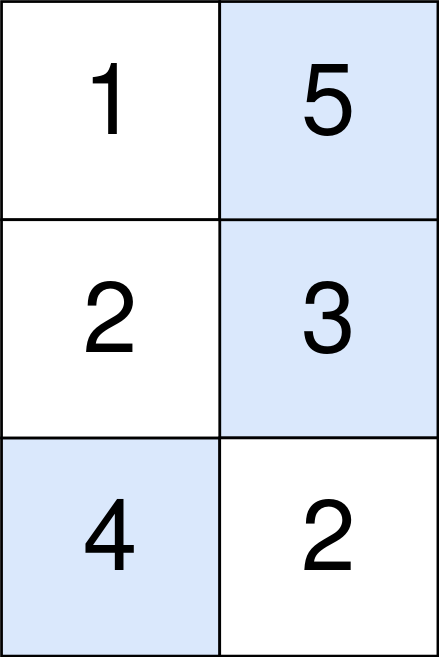
Input: points = [[1,5],[2,3],[4,2]]
Output: 11
Explanation:
The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.
Constraints:
m == points.lengthn == points[r].length1 <= m, n <= 10^51 <= m * n <= 10^50 <= points[r][c] <= 10^5
Solution
Use dynamic programming. Create a 2D array dp of m rows and n columns, where dp[i][j] represents the maximum number of points at position (i, j). When i = 0, dp[0][j] = points[0][j] for all 0 <= j < n.
For 1 <= i < m, to calculate dp[i][j], the maximum values from the previous row need to be calculated. Let prevRowLeft[j] = dp[i - 1][j] - (n - 1 - j) and prevRowRight[j] = dp[i - 1][j] - j. Let leftMax[j] be the maximum from prevRowLeft[0] to prevRowLeft[j] and rightMax[j] be the maximum from prevRowRight[j] to prevRowRight[n - 1]. Then for dp[i][j], the value is calculated as Math.max(leftMax[j] + n - 1 - j, rightMax[j] + j) + points[i][j].
Finally, return the maximum value in dp[m - 1].
-
class Solution { public long maxPoints(int[][] points) { int m = points.length, n = points[0].length; long[][] dp = new long[m][n]; for (int j = 0; j < n; j++) dp[0][j] = points[0][j]; for (int i = 1; i < m; i++) { long[] prevRowLeft = new long[n]; System.arraycopy(dp[i - 1], 0, prevRowLeft, 0, n); for (int j = n - 2; j >= 0; j--) prevRowLeft[j] -= n - 1 - j; long[] prevRowRight = new long[n]; System.arraycopy(dp[i - 1], 0, prevRowRight, 0, n); for (int j = 1; j < n; j++) prevRowRight[j] -= j; long[] leftMax = new long[n]; leftMax[0] = prevRowLeft[0]; for (int j = 1; j < n; j++) leftMax[j] = Math.max(leftMax[j - 1], prevRowLeft[j]); long[] rightMax = new long[n]; rightMax[n - 1] = prevRowRight[n - 1]; for (int j = n - 2; j >= 0; j--) rightMax[j] = Math.max(rightMax[j + 1], prevRowRight[j]); for (int j = 0; j < n; j++) { long curLeftMax = leftMax[j] + n - 1 - j; long curRightMax = rightMax[j] + j; dp[i][j] = Math.max(curLeftMax, curRightMax) + points[i][j]; } } long maxScore = 0; for (int j = 0; j < n; j++) maxScore = Math.max(maxScore, dp[m - 1][j]); return maxScore; } } -
// OJ: https://leetcode.com/problems/maximum-number-of-points-with-cost/ // Time: O(MN) // Space: O(N) class Solution { public: long long maxPoints(vector<vector<int>>& A) { int M = A.size(), N = A[0].size(); vector<long long> dp(N); for (int i = 0; i < N; ++i) dp[i] = A[0][i]; for (int i = 1; i < M; ++i) { vector<long long> next(N); long long mx = dp[0]; for (int j = 0; j < N; ++j) { mx = max(mx, dp[j] + j); next[j] = A[i][j] - j + mx; } mx = dp[N - 1] - (N - 1); for (int j = N - 1; j >= 0; --j) { mx = max(mx, dp[j] - j); next[j] = max(next[j], A[i][j] + j + mx); } swap(next, dp); } return *max_element(begin(dp), end(dp)); } }; -
# 1937. Maximum Number of Points with Cost # https://leetcode.com/problems/maximum-number-of-points-with-cost class Solution: def maxPoints(self, points: List[List[int]]) -> int: rows, cols = len(points), len(points[0]) dp = copy.deepcopy(points) for i in range(rows): for j in range(cols): if i >= 1: dp[i][j] = max(dp[i][j], dp[i - 1][j] + points[i][j]) for j in range(cols): if j > 0: dp[i][j] = max(dp[i][j], dp[i][j - 1] - 1) for j in range(cols)[::-1]: if j + 1 < cols: dp[i][j] = max(dp[i][j], dp[i][j + 1] - 1) return max(dp[-1]) -
func maxPoints(points [][]int) (ans int64) { n := len(points[0]) const inf int64 = 1e18 f := make([]int64, n) for _, p := range points { g := make([]int64, n) lmx, rmx := -inf, -inf for j := range p { lmx = max(lmx, f[j]+int64(j)) g[j] = max(g[j], int64(p[j])+lmx-int64(j)) } for j := n - 1; j >= 0; j-- { rmx = max(rmx, f[j]-int64(j)) g[j] = max(g[j], int64(p[j])+rmx+int64(j)) } f = g } for _, x := range f { ans = max(ans, x) } return } func max(a, b int64) int64 { if a > b { return a } return b } -
function maxPoints(points: number[][]): number { const n = points[0].length; const f: number[] = new Array(n).fill(0); for (const p of points) { const g: number[] = new Array(n).fill(0); let lmx = -Infinity; let rmx = -Infinity; for (let j = 0; j < n; ++j) { lmx = Math.max(lmx, f[j] + j); g[j] = Math.max(g[j], p[j] + lmx - j); } for (let j = n - 1; ~j; --j) { rmx = Math.max(rmx, f[j] - j); g[j] = Math.max(g[j], p[j] + rmx + j); } f.splice(0, n, ...g); } return Math.max(...f); }