Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1924.html

1924. Erect the Fence II

Level

Hard

Description

You are given a 2D integer array trees where trees[i] = [x_i, y_i] represents the location of the i-th tree in the garden.

You are asked to fence the entire garden using the minimum length of rope possible. The garden is well-fenced only if all the trees are enclosed and the rope used forms a perfect circle. A tree is considered enclosed if it is inside or on the border of the circle.

More formally, you must form a circle using the rope with a center (x, y) and radius r where all trees lie inside or on the circle and r is minimum.

Return the center and radius of the circle as a length 3 array [x, y, r]. Answers within 10-5 of the actual answer will be accepted.

Example 1:

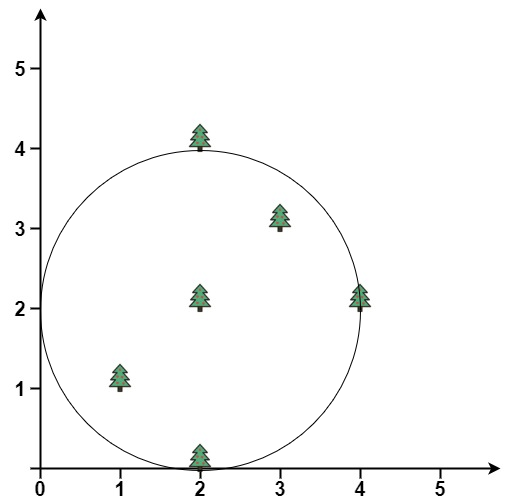
Image text

Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]

Output: [2.00000,2.00000,2.00000]

Explanation: The fence will have center = (2, 2) and radius = 2

Example 2:

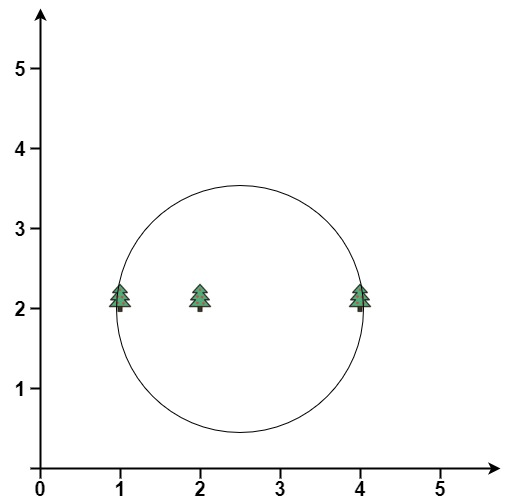
Image text

Input: trees = [[1,2],[2,2],[4,2]]

Output: [2.50000,2.00000,1.50000]

Explanation: The fence will have center = (2.5, 2) and radius = 1.5

Constraints:

  • 1 <= trees.length <= 3000
  • trees[i].length == 2
  • 0 <= x_i, y_i <= 3000

Solution

This problem is the smallest-circle problem. Use Welzl’s algorithm to find the smallest circle’s center and radius.

  • class Solution {
    public double[] outerTrees(int[][] trees) {
        double radius = 0.0;
        double x = trees[0][0], y = trees[0][1];
        int length = trees.length;
        for (int i = 1; i < length; i++) {
            if (getSquaredDistance(trees[i][0], x, trees[i][1], y) > radius * radius) {
                x = trees[i][0];
                y = trees[i][1];
                radius = 0.0;
                for (int j = 0; j < i; j++) {
                    if (getSquaredDistance(trees[j][0], x, trees[j][1], y) > radius * radius) {
                        x = (trees[i][0] + trees[j][0]) / 2.0;
                        y = (trees[i][1] + trees[j][1]) / 2.0;
                        radius = Math.sqrt(getSquaredDistance(x, trees[j][0], y, trees[j][1]));
                        for (int k = 0; k < j; k++) {
                            if (getSquaredDistance(trees[k][0], x, trees[k][1], y) > radius * radius) {
                                double[] circle = getCircle(trees, i, j, k);
                                x = circle[0];
                                y = circle[1];
                                radius = circle[2];
                            }
                        }
                    }
                }
            }
        }
        return new double[]{x, y, radius};
    }

    public double[] getCircle(int[][] trees, int i, int j, int k) {
        double p1 = trees[i][1] - trees[k][1], p2 = trees[i][1] - trees[j][1];
        double q1 = trees[i][0] - trees[k][0], q2 = trees[i][0] - trees[j][0];
        double a = (trees[i][0] * trees[i][0] - trees[j][0] * trees[j][0]) + (trees[i][1] * trees[i][1] - trees[j][1] * trees[j][1]);
        double b = (trees[i][0] * trees[i][0] - trees[k][0] * trees[k][0]) + (trees[i][1] * trees[i][1] - trees[k][1] * trees[k][1]);
        double c = 2 * (trees[i][0] - trees[j][0]) * (trees[i][1] - trees[k][1]) - 2 * (trees[i][0] - trees[k][0]) * (trees[i][1] - trees[j][1]);
        double x = (p1 * a - p2 * b) / c;
        double y = (q2 * b - q1 * a) / c;
        double radius = Math.sqrt(getSquaredDistance(trees[k][0], x, trees[k][1], y));
        return new double[]{x, y, radius};
    }

    public double getSquaredDistance(double x1, double x2, double y1, double y2) {
        return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
    }
}

All Problems

All Solutions