Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1902.html

1902. Depth of BST Given Insertion Order

Level

Medium

Description

You are given a 0-indexed integer array order of length n, a permutation of integers from 1 to n representing the order of insertion into a binary search tree.

A binary search tree is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

The binary search tree is constructed as follows:

• order[0] will be the root of the binary search tree.
• All subsequent elements are inserted as the child of any existing node such that the binary search tree properties hold.

Return the depth of the binary search tree.

A binary tree’s depth8* is the number of **nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

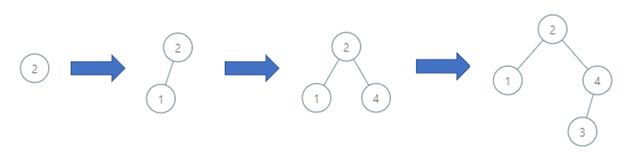
Input: order = [2,1,4,3]

Output: 3

Explanation: The binary search tree has a depth of 3 with path 2->3->4.

Example 2:

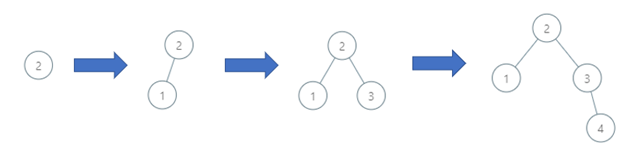
Input: order = [2,1,3,4]

Output: 3

Explanation: The binary search tree has a depth of 3 with path 2->3->4.

Example 3:

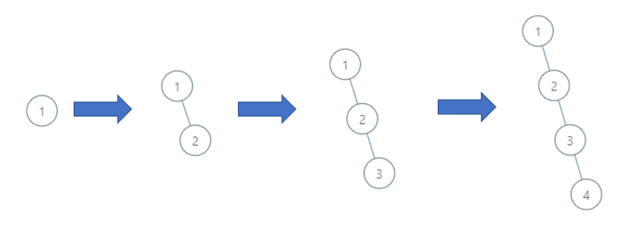
Input: order = [1,2,3,4]

Output: 4

Explanation: The binary search tree has a depth of 4 with path 1->2->3->4.

Constraints:

• n == order.length
• 1 <= n <= 10^5
• order is a permutation of integers between 1 and n.

Solution

Use a TreeMap to store each value’s depth. Initially, value order[0] has depth 1.

Loop over the remaining elements in order. For each value curr, find the two adjacent values of curr in the TreeMap, which are prev and next such that prev <= curr <= next. If both values exist (not null), then since both prev and next come before curr, the depth of curr is the maximum of the depths of prev and next plus 1. If only one value exists, then the depth of curr is the depth of the existing value plus 1.

Maintain the maximum depth during the process. Finally, return the maximum depth.

• Java
• Python

• class Solution {
      public int maxDepthBST(int[] order) {
          TreeMap<Integer, Integer> depthMap = new TreeMap<Integer, Integer>();
          depthMap.put(order[0], 1);
          int maxDepth = 1;
          int length = order.length;
          for (int i = 1; i < length; i++) {
              int curr = order[i];
              Integer prev = depthMap.floorKey(curr - 1);
              Integer next = depthMap.ceilingKey(curr + 1);
              int currDepth = 0;
              if (prev != null && next != null)
                  currDepth = Math.max(depthMap.get(prev), depthMap.get(next)) + 1;
              else if (prev != null)
                  currDepth = depthMap.get(prev) + 1;
              else
                  currDepth = depthMap.get(next) + 1;
              depthMap.put(curr, currDepth);
              maxDepth = Math.max(maxDepth, currDepth);
          }
          return maxDepth;
      }
  }
  
  ############
  
  class Solution {
      public int maxDepthBST(int[] order) {
          TreeMap<Integer, Integer> tm = new TreeMap<>();
          tm.put(0, 0);
          tm.put(Integer.MAX_VALUE, 0);
          tm.put(order[0], 1);
          int ans = 1;
          for (int i = 1; i < order.length; ++i) {
              int v = order[i];
              Map.Entry<Integer, Integer> lower = tm.lowerEntry(v);
              Map.Entry<Integer, Integer> higher = tm.higherEntry(v);
              int depth = 1 + Math.max(lower.getValue(), higher.getValue());
              ans = Math.max(ans, depth);
              tm.put(v, depth);
          }
          return ans;
      }
  }
  

• from sortedcontainers import SortedDict
  
  
  class Solution:
      def maxDepthBST(self, order: List[int]) -> int:
          sd = SortedDict({0: 0, inf: 0, order[0]: 1})
          ans = 1
          for v in order[1:]:
              lower = sd.bisect_left(v) - 1
              higher = lower + 1
              depth = 1 + max(sd.values()[lower], sd.values()[higher])
              ans = max(ans, depth)
              sd[v] = depth
          return ans
  
  
  

All Problems

All Solutions