Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1901.html

1901. Find a Peak Element II

Level

Medium

Description

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

Example 1:

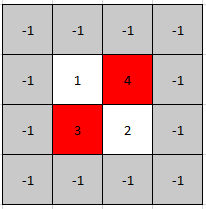
Input: mat = [[1,4],[3,2]]

Output: [0,1]

Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

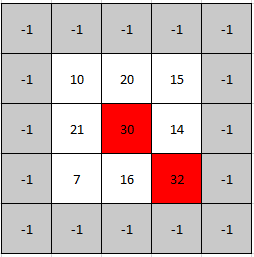
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]

Output: [1,1]

Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 10^5
• No two adjacent cells are equal.

Solution

Use binary search. Initialize low = 0 and high = m - 1. Each time let mid be the mean of low and high, and find maxIndex such that mat[mid][maxIndex] is the greatest element in the row mat[mid]. If mat[mid][maxIndex] < mat[mid + 1][maxIndex], then let low = mid + 1. Otherwise, let high = mid.

When the row is determined using binary search, find the greatest element in the row and get the column index of the greatest element. Return the row index and the column index.

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public int[] findPeakGrid(int[][] mat) {
          int m = mat.length, n = mat[0].length;
          int low = 0, high = m - 1, maxIndex = 0;
          while (low < high) {
              int mid = (high - low) / 2 + low;
              maxIndex = getMaxIndex(mat[mid], n);
              if (mat[mid][maxIndex] < mat[mid + 1][maxIndex])
                  low = mid + 1;
              else
                  high = mid;
          }
  		maxIndex = getMaxIndex(mat[low], n);
          return new int[]{low, maxIndex};
      }
      
      public int getMaxIndex(int[] arr, int n) {
          int index = 0, maxNum = 0;
          for (int i = 0; i < n; i++) {
              if (maxNum < arr[i]) {
                  maxNum = arr[i];
                  index = i;
              }
          }
          return index;
      }
  }
  

• // OJ: https://leetcode.com/problems/find-a-peak-element-ii/
  // Time: O(NlogM)
  // Space: O(1)
  class Solution {
  public:
      vector<int> findPeakGrid(vector<vector<int>>& A) {
          int M = A.size(), N = A[0].size(), L = 0, R = M - 1;
          while (L < R) {
              int mid = (L + R + 1) / 2;
              int left = mid - 1 >= 0 ? *max_element(begin(A[mid - 1]), end(A[mid - 1])) : -1;
              int cur = *max_element(begin(A[mid]), end(A[mid]));
              if (cur > left) L = mid;
              else R = mid - 1;
          }
          return { L, int(max_element(begin(A[L]), end(A[L])) - begin(A[L])) };
      }
  };
  

• class Solution:
      def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
          l, r = 0, len(mat) - 1
          while l < r:
              mid = (l + r) >> 1
              j = mat[mid].index(max(mat[mid]))
              if mat[mid][j] > mat[mid + 1][j]:
                  r = mid
              else:
                  l = mid + 1
          return [l, mat[l].index(max(mat[l]))]
  
  

• func findPeakGrid(mat [][]int) []int {
  	maxPos := func(arr []int) int {
  		j := 0
  		for i := 1; i < len(arr); i++ {
  			if arr[i] > arr[j] {
  				j = i
  			}
  		}
  		return j
  	}
  	l, r := 0, len(mat)-1
  	for l < r {
  		mid := (l + r) >> 1
  		j := maxPos(mat[mid])
  		if mat[mid][j] > mat[mid+1][j] {
  			r = mid
  		} else {
  			l = mid + 1
  		}
  	}
  	return []int{l, maxPos(mat[l])}
  }
  

• function findPeakGrid(mat: number[][]): number[] {
      let [l, r] = [0, mat.length - 1];
      while (l < r) {
          const mid = (l + r) >> 1;
          const j = mat[mid].indexOf(Math.max(...mat[mid]));
          if (mat[mid][j] > mat[mid + 1][j]) {
              r = mid;
          } else {
              l = mid + 1;
          }
      }
      return [l, mat[l].indexOf(Math.max(...mat[l]))];
  }
  
  

• impl Solution {
      pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> {
          let mut l: usize = 0;
          let mut r: usize = mat.len() - 1;
          while l < r {
              let mid: usize = (l + r) >> 1;
              let j: usize = mat[mid]
                  .iter()
                  .position(|&x| x == *mat[mid].iter().max().unwrap())
                  .unwrap();
              if mat[mid][j] > mat[mid + 1][j] {
                  r = mid;
              } else {
                  l = mid + 1;
              }
          }
          let j: usize = mat[l]
              .iter()
              .position(|&x| x == *mat[l].iter().max().unwrap())
              .unwrap();
          vec![l as i32, j as i32]
      }
  }
  
  

All Problems

All Solutions