Welcome to Subscribe On Youtube
2065. Maximum Path Quality of a Graph
Description
There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the ith node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [uj, vj, timej] indicates that there is an undirected edge between the nodes uj and vj, and it takes timej seconds to travel between the two nodes. Finally, you are given an integer maxTime.
A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node's value is added at most once to the sum).
Return the maximum quality of a valid path.
Note: There are at most four edges connected to each node.
Example 1:
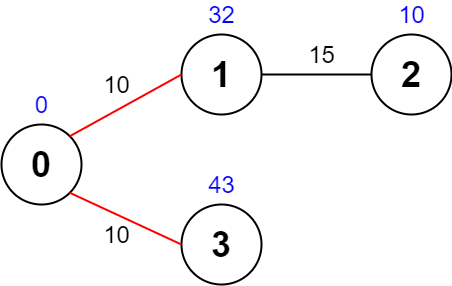
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49 Output: 75 Explanation: One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49. The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.
Example 2:
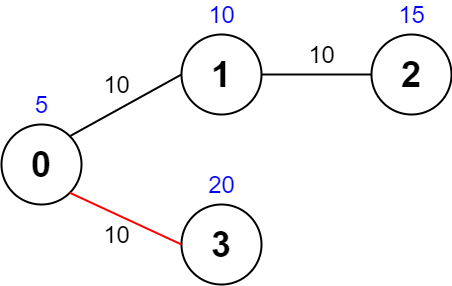
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30 Output: 25 Explanation: One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30. The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.
Example 3:
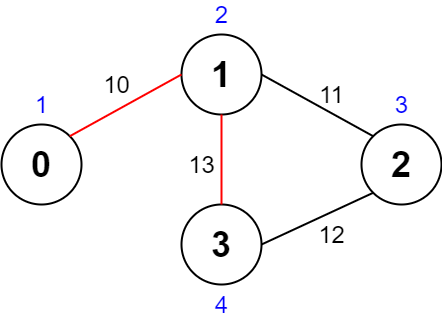
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50 Output: 7 Explanation: One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50. The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.
Constraints:
n == values.length1 <= n <= 10000 <= values[i] <= 1080 <= edges.length <= 2000edges[j].length == 30 <= uj < vj <= n - 110 <= timej, maxTime <= 100- All the pairs
[uj, vj]are unique. - There are at most four edges connected to each node.
- The graph may not be connected.
Solutions
-
function maximalPathQuality(values: number[], edges: number[][], maxTime: number): number { const n = values.length; let g: Array<Array<Array<number>>> = Array.from({ length: n }, v => new Array()); for (let edge of edges) { let [u, v, t] = edge; g[u].push([v, t]); g[v].push([u, t]); } let visited = new Array(n).fill(false); let ans = 0; function dfs(u: number, time: number, value: number): void { // 索引0为终点 if (!u) { ans = Math.max(value, ans); } for (let [v, dist] of g[u]) { if (time - dist >= 0) { if (!visited[v]) { visited[v] = true; dfs(v, time - dist, value + values[v]); visited[v] = false; // 回溯 } else { dfs(v, time - dist, value); } } } } // 索引0为起点 visited[0] = true; dfs(0, maxTime, values[0]); return ans; } -
class Solution { private List<int[]>[] g; private boolean[] vis; private int[] values; private int maxTime; private int ans; public int maximalPathQuality(int[] values, int[][] edges, int maxTime) { int n = values.length; g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : edges) { int u = e[0], v = e[1], t = e[2]; g[u].add(new int[] {v, t}); g[v].add(new int[] {u, t}); } vis = new boolean[n]; vis[0] = true; this.values = values; this.maxTime = maxTime; dfs(0, 0, values[0]); return ans; } private void dfs(int u, int cost, int value) { if (u == 0) { ans = Math.max(ans, value); } for (var e : g[u]) { int v = e[0], t = e[1]; if (cost + t <= maxTime) { if (vis[v]) { dfs(v, cost + t, value); } else { vis[v] = true; dfs(v, cost + t, value + values[v]); vis[v] = false; } } } } } -
class Solution { public: int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) { int n = values.size(); vector<pair<int, int>> g[n]; for (auto& e : edges) { int u = e[0], v = e[1], t = e[2]; g[u].emplace_back(v, t); g[v].emplace_back(u, t); } bool vis[n]; memset(vis, false, sizeof(vis)); vis[0] = true; int ans = 0; auto dfs = [&](auto&& dfs, int u, int cost, int value) -> void { if (u == 0) { ans = max(ans, value); } for (auto& [v, t] : g[u]) { if (cost + t <= maxTime) { if (vis[v]) { dfs(dfs, v, cost + t, value); } else { vis[v] = true; dfs(dfs, v, cost + t, value + values[v]); vis[v] = false; } } } }; dfs(dfs, 0, 0, values[0]); return ans; } }; -
class Solution: def maximalPathQuality( self, values: List[int], edges: List[List[int]], maxTime: int ) -> int: def dfs(u: int, cost: int, value: int): if u == 0: nonlocal ans ans = max(ans, value) for v, t in g[u]: if cost + t <= maxTime: if vis[v]: dfs(v, cost + t, value) else: vis[v] = True dfs(v, cost + t, value + values[v]) vis[v] = False n = len(values) g = [[] for _ in range(n)] for u, v, t in edges: g[u].append((v, t)) g[v].append((u, t)) vis = [False] * n vis[0] = True ans = 0 dfs(0, 0, values[0]) return ans -
func maximalPathQuality(values []int, edges [][]int, maxTime int) (ans int) { n := len(values) g := make([][][2]int, n) for _, e := range edges { u, v, t := e[0], e[1], e[2] g[u] = append(g[u], [2]int{v, t}) g[v] = append(g[v], [2]int{u, t}) } vis := make([]bool, n) vis[0] = true var dfs func(u, cost, value int) dfs = func(u, cost, value int) { if u == 0 { ans = max(ans, value) } for _, e := range g[u] { v, t := e[0], e[1] if cost+t <= maxTime { if vis[v] { dfs(v, cost+t, value) } else { vis[v] = true dfs(v, cost+t, value+values[v]) vis[v] = false } } } } dfs(0, 0, values[0]) return }