Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1886.html
1886. Determine Whether Matrix Can Be Obtained By Rotation
Level
Easy
Description
Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.
Example 1:
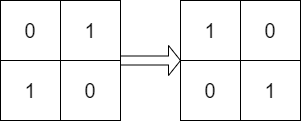
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.
Example 2:
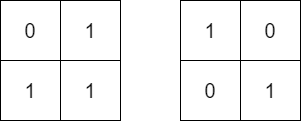
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
Output: false
Explanation: It is impossible to make mat equal to target by rotating mat.
Example 3:
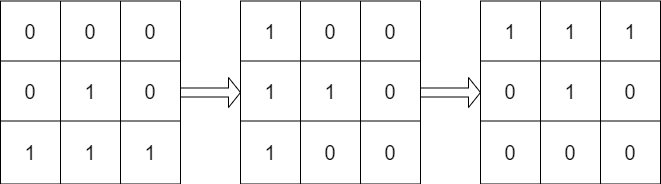
Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.
Constraints:
n == mat.length == target.lengthn == mat[i].length == target[i].length1 <= n <= 10mat[i][j]andtarget[i][j]are either0or1.
Solution
Let rotate be the state of mat after rotating 90 degrees clockwise. For 0 <= i < n and 0 <= j < n, there is rotate[j][n - 1 - i] = mat[i][j]. Since rotating the matrix 4 times makes the matrix recover to the original state, the matrix can be rotated at most 4 times. Therefore, rotate the matrix 1, 2, 3 and 4 times respecitvely, and for each state, check whether the state is the same as target. If there exists one state that is the same as target, return true. Otherwise, return false.
-
class Solution { public boolean findRotation(int[][] mat, int[][] target) { int n = mat.length; int[][] rotate = new int[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) rotate[i][j] = mat[i][j]; } for (int count = 1; count <= 4; count++) { int[][] temp = new int[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) temp[j][n - 1 - i] = rotate[i][j]; } rotate = temp; if (areSame(rotate, target)) return true; } return false; } public boolean areSame(int[][] mat, int[][] target) { int n = mat.length; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (mat[i][j] != target[i][j]) return false; } } return true; } } ############ class Solution { public boolean findRotation(int[][] mat, int[][] target) { int n = mat.length; for (int k = 0; k < 4; ++k) { int[][] g = new int[n][n]; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { g[i][j] = mat[j][n - i - 1]; } } if (equals(g, target)) { return true; } mat = g; } return false; } private boolean equals(int[][] a, int[][] b) { int n = a.length; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (a[i][j] != b[i][j]) { return false; } } } return true; } } -
// OJ: https://leetcode.com/problems/determine-whether-matrix-can-be-obtained-by-rotation/ // Time: O(N^2) // Space: O(1) class Solution { void rotate(vector<vector<int>> &A) { int N = A.size(); for (int i = 0; i < N / 2; ++i) { for (int j = i; j < N - i - 1; ++j) { int tmp = A[i][j]; A[i][j] = A[j][N - i - 1]; A[j][N - i - 1] = A[N - i - 1][N - j - 1]; A[N - i - 1][N - j - 1] = A[N - j - 1][i]; A[N - j - 1][i] = tmp; } } } public: bool findRotation(vector<vector<int>>& A, vector<vector<int>>& B) { if (A == B) return true; for (int i = 0; i < 3; ++i) { rotate(A); if (A == B) return true; } return false; } }; -
class Solution: def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool: for _ in range(4): mat = [list(col) for col in zip(*mat[::-1])] if mat == target: return True return False ############ # 1886. Determine Whether Matrix Can Be Obtained By Rotation # https://leetcode.com/problems/determine-whether-matrix-can-be-obtained-by-rotation/ class Solution: def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool: for _ in range(4): if mat == target: return True mat = [list(x) for x in zip(*mat[::-1])] return False -
func findRotation(mat [][]int, target [][]int) bool { n := len(mat) for k := 0; k < 4; k++ { g := make([][]int, n) for i := range g { g[i] = make([]int, n) } for i := 0; i < n; i++ { for j := 0; j < n; j++ { g[i][j] = mat[j][n-i-1] } } if equals(g, target) { return true } mat = g } return false } func equals(a, b [][]int) bool { for i, row := range a { for j, v := range row { if v != b[i][j] { return false } } } return true } -
function findRotation(mat: number[][], target: number[][]): boolean { for (let k = 0; k < 4; k++) { rotate(mat); if (isEqual(mat, target)) { return true; } } return false; } function isEqual(A: number[][], B: number[][]) { const n = A.length; for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { if (A[i][j] !== B[i][j]) { return false; } } } return true; } function rotate(matrix: number[][]): void { const n = matrix.length; for (let i = 0; i < n >> 1; i++) { for (let j = 0; j < (n + 1) >> 1; j++) { [ matrix[i][j], matrix[n - 1 - j][i], matrix[n - 1 - i][n - 1 - j], matrix[j][n - 1 - i], ] = [ matrix[n - 1 - j][i], matrix[n - 1 - i][n - 1 - j], matrix[j][n - 1 - i], matrix[i][j], ]; } } } -
impl Solution { pub fn find_rotation(mat: Vec<Vec<i32>>, target: Vec<Vec<i32>>) -> bool { let n = mat.len(); let mut is_equal = [true; 4]; for i in 0..n { for j in 0..n { if is_equal[0] && mat[i][j] != target[i][j] { is_equal[0] = false; } if is_equal[1] && mat[i][j] != target[j][n - 1 - i] { is_equal[1] = false; } if is_equal[2] && mat[i][j] != target[n - 1 - i][n - 1 - j] { is_equal[2] = false; } if is_equal[3] && mat[i][j] != target[n - 1 - j][i] { is_equal[3] = false; } } } is_equal.into_iter().any(|&v| v) } }