Formatted question description: https://leetcode.ca/all/1878.html

1878. Get Biggest Three Rhombus Sums in a Grid

Level

Medium

Description

You are given an m x n integer matrix grid.

A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:

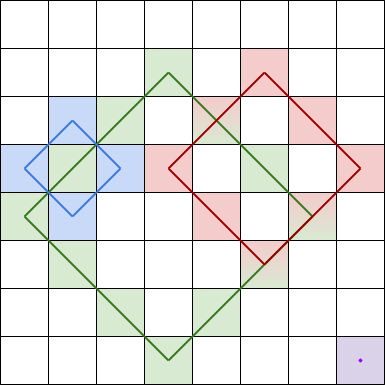
Image text

Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.

Return the biggest three distinct rhombus sums in the grid in descending order. If there are less than three distinct values, return all of them.

Example 1:

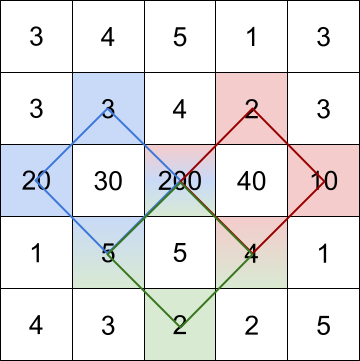
Image text

Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]

Output: [228,216,211]

Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.

Blue: 20 + 3 + 200 + 5 = 228
Red: 200 + 2 + 10 + 4 = 216
Green: 5 + 200 + 4 + 2 = 211

Example 2:

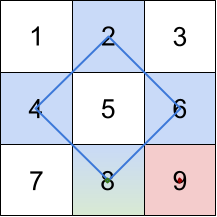
Image text

Input: grid = [[1,2,3],[4,5,6],[7,8,9]]

Output: [20,9,8]

Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.

Blue: 4 + 2 + 6 + 8 = 20
Red: 9 (area 0 rhombus in the bottom right corner)
Green: 8 (area 0 rhombus in the bottom middle)

Example 3:

Input: grid = [[7,7,7]]

Output: [7]

Explanation: All three possible rhombus sums are the same, so return [7].

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 10^5

Solution

Loop over all possible rhombuses. For each rhombus, calculate the rhombus sum. Use a tree set to store the rhombus sums and only keep the three biggest rhombus sums. Finally, use an array to store the biggest rhombus sums in descending order and return.

class Solution {
    public int[] getBiggestThree(int[][] grid) {
        int rows = grid.length, columns = grid[0].length;
        int maxSide = (Math.min(rows, columns) + 1) / 2;
        TreeSet<Integer> set = new TreeSet<Integer>();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                set.add(grid[i][j]);
                if (set.size() > 3)
                    set.remove(set.first());
            }
        }
        for (int side = 2; side <= maxSide; side++) {
            int rowStart = 0, rowEnd = rows - (side * 2 - 1);
            int columnStart = side - 1, columnEnd = columns - side;
            for (int i = rowStart; i <= rowEnd; i++) {
                for (int j = columnStart; j <= columnEnd; j++) {
                    int sum = getSum(grid, i, j, side);
                    set.add(sum);
                    if (set.size() > 3)
                        set.remove(set.first());
                }
            }
        }
        List<Integer> list = new ArrayList<Integer>(set);
        Collections.reverse(list);
        int size = list.size();
        int[] biggest = new int[size];
        for (int i = 0; i < size; i++)
            biggest[i] = list.get(i);
        return biggest;
    }

    public int getSum(int[][] grid, int topRow, int topColumn, int side) {
        int bottomRow = topRow + (side - 1) * 2;
        int sum = grid[topRow][topColumn] + grid[bottomRow][topColumn];
        for (int i = 1; i < side; i++)
            sum += grid[topRow + i][topColumn - i] + grid[topRow + i][topColumn + i];
        for (int i = 1; i < side - 1; i++)
            sum += grid[bottomRow - i][topColumn - i] + grid[bottomRow - i][topColumn + i];
        return sum;
    }
}

// OJ: https://leetcode.com/problems/get-biggest-three-rhombus-sums-in-a-grid/
// Time: O(MN * min(M, N))
// Space: O(1)
class Solution {
public:
    vector<int> getBiggestThree(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size(), dirs[4][2] = { {1,1},{1,-1},{-1,-1},{-1,1} };
        set<int> s;
        for (int len = 1; len * 2 - 1 <= min(M, N); ++len) {
            for (int i = 0; i + 2 * len - 2 < M; ++i) {
                for (int j = len - 1; j <= N - len; ++j) {
                    int x = i, y = j, sum = len == 1 ? A[x][y] : 0;
                    for (auto &[dx, dy] : dirs) {
                        for (int k = 0; k < len - 1; ++k) {
                            sum += A[x += dx][y += dy];
                        }
                    }
                    s.insert(sum);
                    if (s.size() > 3) s.erase(s.begin());
                }
            }
        }
        return vector<int>(rbegin(s), rend(s));
    }
};

# 1878. Get Biggest Three Rhombus Sums in a Grid
# https://leetcode.com/problems/get-biggest-three-rhombus-sums-in-a-grid

class Solution:
    def getBiggestThree(self, grid: List[List[int]]) -> List[int]:
        rows, cols = len(grid), len(grid[0])
        res = set()
        
        def isValid(pos):
            return 0 <= pos[0] < rows and 0 <= pos[1] < cols
        
        def calculateTotal(lst, size):
            top, left, right, bottom = lst
            x, y = top
            total = grid[top[0]][top[1]] + grid[bottom[0]][bottom[1]] if size > 0 else grid[top[0]][top[1]]
            
            for i in range(1, size + 1):
                l = (x + i, y - i)
                r = (x + i, y + i)
                total += (grid[l[0]][l[1]] + grid[r[0]][r[1]])
            
            if size > 1:
                x, y = bottom
                for i in range(1, size):
                    l = (x - i, y + i)
                    r = (x - i, y - i)
                    total += (grid[l[0]][l[1]] + grid[r[0]][r[1]])
            
            return total
        
        def dfs(x, y, size):
            top = (x, y)
            left = (x + size, y - size)
            right = (x + size, y + size)
            bottom = (x + (size * 2) , y) if size != 0 else top
            
            lst = [top, left, right, bottom]
            
            if all(isValid(pos) for pos in lst):
                total = calculateTotal(lst, size)
                res.add(total)
                dfs(x, y, size + 1)
        
        for i in range(rows):
            for j in range(cols):
                dfs(i, j, 0)
        
        return sorted(list(res))[::-1][:3]

func getBiggestThree(grid [][]int) []int {
	m, n := len(grid), len(grid[0])
	s1 := make([][]int, m+1)
	s2 := make([][]int, m+1)
	for i := range s1 {
		s1[i] = make([]int, n+2)
		s2[i] = make([]int, n+2)
	}
	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			s1[i][j] = s1[i-1][j-1] + grid[i-1][j-1]
			s2[i][j] = s2[i-1][j+1] + grid[i-1][j-1]
		}
	}

	ss := treemap.NewWithIntComparator()
	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			l := min(i-1, m-i, j-1, n-j)
			ss.Put(grid[i-1][j-1], nil)
			for k := 1; k <= l; k++ {
				a := s1[i+k][j] - s1[i][j-k]
				b := s1[i][j+k] - s1[i-k][j]
				c := s2[i][j-k] - s2[i-k][j]
				d := s2[i+k][j] - s2[i][j+k]
				ss.Put(a+b+c+d-grid[i+k-1][j-1]+grid[i-k-1][j-1], nil)
			}
			for ss.Size() > 3 {
				x, _ := ss.Min()
				ss.Remove(x.(int))
			}
		}
	}
	ans := make([]int, ss.Size())
	for i, k := range ss.Keys() {
		ans[len(ans)-i-1] = k.(int)
	}
	return ans
}

function getBiggestThree(grid: number[][]): number[] {
    const m = grid.length;
    const n = grid[0].length;
    const s1: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0));
    const s2: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0));
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1];
            s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1];
        }
    }
    const ss = new TreeSet<number>();
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            const l = Math.min(i - 1, m - i, j - 1, n - j);
            ss.add(grid[i - 1][j - 1]);
            for (let k = 1; k <= l; ++k) {
                const a = s1[i + k][j] - s1[i][j - k];
                const b = s1[i][j + k] - s1[i - k][j];
                const c = s2[i][j - k] - s2[i - k][j];
                const d = s2[i + k][j] - s2[i][j + k];
                ss.add(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]);
            }
            while (ss.size() > 3) {
                ss.shift();
            }
        }
    }
    return [...ss].reverse();
}

type Compare<T> = (lhs: T, rhs: T) => number;

class RBTreeNode<T = number> {
    data: T;
    count: number;
    left: RBTreeNode<T> | null;
    right: RBTreeNode<T> | null;
    parent: RBTreeNode<T> | null;
    color: number;
    constructor(data: T) {
        this.data = data;
        this.left = this.right = this.parent = null;
        this.color = 0;
        this.count = 1;
    }

    sibling(): RBTreeNode<T> | null {
        if (!this.parent) return null; // sibling null if no parent
        return this.isOnLeft() ? this.parent.right : this.parent.left;
    }

    isOnLeft(): boolean {
        return this === this.parent!.left;
    }

    hasRedChild(): boolean {
        return (
            Boolean(this.left && this.left.color === 0) ||
            Boolean(this.right && this.right.color === 0)
        );
    }
}

class RBTree<T> {
    root: RBTreeNode<T> | null;
    lt: (l: T, r: T) => boolean;
    constructor(compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0)) {
        this.root = null;
        this.lt = (l: T, r: T) => compare(l, r) < 0;
    }

    rotateLeft(pt: RBTreeNode<T>): void {
        const right = pt.right!;
        pt.right = right.left;

        if (pt.right) pt.right.parent = pt;
        right.parent = pt.parent;

        if (!pt.parent) this.root = right;
        else if (pt === pt.parent.left) pt.parent.left = right;
        else pt.parent.right = right;

        right.left = pt;
        pt.parent = right;
    }

    rotateRight(pt: RBTreeNode<T>): void {
        const left = pt.left!;
        pt.left = left.right;

        if (pt.left) pt.left.parent = pt;
        left.parent = pt.parent;

        if (!pt.parent) this.root = left;
        else if (pt === pt.parent.left) pt.parent.left = left;
        else pt.parent.right = left;

        left.right = pt;
        pt.parent = left;
    }

    swapColor(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
        const tmp = p1.color;
        p1.color = p2.color;
        p2.color = tmp;
    }

    swapData(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
        const tmp = p1.data;
        p1.data = p2.data;
        p2.data = tmp;
    }

    fixAfterInsert(pt: RBTreeNode<T>): void {
        let parent = null;
        let grandParent = null;

        while (pt !== this.root && pt.color !== 1 && pt.parent?.color === 0) {
            parent = pt.parent;
            grandParent = pt.parent.parent;

            /*  Case : A
                Parent of pt is left child of Grand-parent of pt */
            if (parent === grandParent?.left) {
                const uncle = grandParent.right;

                /* Case : 1
                   The uncle of pt is also red
                   Only Recoloring required */
                if (uncle && uncle.color === 0) {
                    grandParent.color = 0;
                    parent.color = 1;
                    uncle.color = 1;
                    pt = grandParent;
                } else {
                    /* Case : 2
                       pt is right child of its parent
                       Left-rotation required */
                    if (pt === parent.right) {
                        this.rotateLeft(parent);
                        pt = parent;
                        parent = pt.parent;
                    }

                    /* Case : 3
                       pt is left child of its parent
                       Right-rotation required */
                    this.rotateRight(grandParent);
                    this.swapColor(parent!, grandParent);
                    pt = parent!;
                }
            } else {
                /* Case : B
               Parent of pt is right child of Grand-parent of pt */
                const uncle = grandParent!.left;

                /*  Case : 1
                    The uncle of pt is also red
                    Only Recoloring required */
                if (uncle != null && uncle.color === 0) {
                    grandParent!.color = 0;
                    parent.color = 1;
                    uncle.color = 1;
                    pt = grandParent!;
                } else {
                    /* Case : 2
                       pt is left child of its parent
                       Right-rotation required */
                    if (pt === parent.left) {
                        this.rotateRight(parent);
                        pt = parent;
                        parent = pt.parent;
                    }

                    /* Case : 3
                       pt is right child of its parent
                       Left-rotation required */
                    this.rotateLeft(grandParent!);
                    this.swapColor(parent!, grandParent!);
                    pt = parent!;
                }
            }
        }
        this.root!.color = 1;
    }

    delete(val: T): boolean {
        const node = this.find(val);
        if (!node) return false;
        node.count--;
        if (!node.count) this.deleteNode(node);
        return true;
    }

    deleteAll(val: T): boolean {
        const node = this.find(val);
        if (!node) return false;
        this.deleteNode(node);
        return true;
    }

    deleteNode(v: RBTreeNode<T>): void {
        const u = BSTreplace(v);

        // True when u and v are both black
        const uvBlack = (u === null || u.color === 1) && v.color === 1;
        const parent = v.parent!;

        if (!u) {
            // u is null therefore v is leaf
            if (v === this.root) this.root = null;
            // v is root, making root null
            else {
                if (uvBlack) {
                    // u and v both black
                    // v is leaf, fix double black at v
                    this.fixDoubleBlack(v);
                } else {
                    // u or v is red
                    if (v.sibling()) {
                        // sibling is not null, make it red"
                        v.sibling()!.color = 0;
                    }
                }
                // delete v from the tree
                if (v.isOnLeft()) parent.left = null;
                else parent.right = null;
            }
            return;
        }

        if (!v.left || !v.right) {
            // v has 1 child
            if (v === this.root) {
                // v is root, assign the value of u to v, and delete u
                v.data = u.data;
                v.left = v.right = null;
            } else {
                // Detach v from tree and move u up
                if (v.isOnLeft()) parent.left = u;
                else parent.right = u;
                u.parent = parent;
                if (uvBlack) this.fixDoubleBlack(u);
                // u and v both black, fix double black at u
                else u.color = 1; // u or v red, color u black
            }
            return;
        }

        // v has 2 children, swap data with successor and recurse
        this.swapData(u, v);
        this.deleteNode(u);

        // find node that replaces a deleted node in BST
        function BSTreplace(x: RBTreeNode<T>): RBTreeNode<T> | null {
            // when node have 2 children
            if (x.left && x.right) return successor(x.right);
            // when leaf
            if (!x.left && !x.right) return null;
            // when single child
            return x.left ?? x.right;
        }
        // find node that do not have a left child
        // in the subtree of the given node
        function successor(x: RBTreeNode<T>): RBTreeNode<T> {
            let temp = x;
            while (temp.left) temp = temp.left;
            return temp;
        }
    }

    fixDoubleBlack(x: RBTreeNode<T>): void {
        if (x === this.root) return; // Reached root

        const sibling = x.sibling();
        const parent = x.parent!;
        if (!sibling) {
            // No sibiling, double black pushed up
            this.fixDoubleBlack(parent);
        } else {
            if (sibling.color === 0) {
                // Sibling red
                parent.color = 0;
                sibling.color = 1;
                if (sibling.isOnLeft()) this.rotateRight(parent);
                // left case
                else this.rotateLeft(parent); // right case
                this.fixDoubleBlack(x);
            } else {
                // Sibling black
                if (sibling.hasRedChild()) {
                    // at least 1 red children
                    if (sibling.left && sibling.left.color === 0) {
                        if (sibling.isOnLeft()) {
                            // left left
                            sibling.left.color = sibling.color;
                            sibling.color = parent.color;
                            this.rotateRight(parent);
                        } else {
                            // right left
                            sibling.left.color = parent.color;
                            this.rotateRight(sibling);
                            this.rotateLeft(parent);
                        }
                    } else {
                        if (sibling.isOnLeft()) {
                            // left right
                            sibling.right!.color = parent.color;
                            this.rotateLeft(sibling);
                            this.rotateRight(parent);
                        } else {
                            // right right
                            sibling.right!.color = sibling.color;
                            sibling.color = parent.color;
                            this.rotateLeft(parent);
                        }
                    }
                    parent.color = 1;
                } else {
                    // 2 black children
                    sibling.color = 0;
                    if (parent.color === 1) this.fixDoubleBlack(parent);
                    else parent.color = 1;
                }
            }
        }
    }

    insert(data: T): boolean {
        // search for a position to insert
        let parent = this.root;
        while (parent) {
            if (this.lt(data, parent.data)) {
                if (!parent.left) break;
                else parent = parent.left;
            } else if (this.lt(parent.data, data)) {
                if (!parent.right) break;
                else parent = parent.right;
            } else break;
        }

        // insert node into parent
        const node = new RBTreeNode(data);
        if (!parent) this.root = node;
        else if (this.lt(node.data, parent.data)) parent.left = node;
        else if (this.lt(parent.data, node.data)) parent.right = node;
        else {
            parent.count++;
            return false;
        }
        node.parent = parent;
        this.fixAfterInsert(node);
        return true;
    }

    find(data: T): RBTreeNode<T> | null {
        let p = this.root;
        while (p) {
            if (this.lt(data, p.data)) {
                p = p.left;
            } else if (this.lt(p.data, data)) {
                p = p.right;
            } else break;
        }
        return p ?? null;
    }

    *inOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
        if (!root) return;
        for (const v of this.inOrder(root.left!)) yield v;
        yield root.data;
        for (const v of this.inOrder(root.right!)) yield v;
    }

    *reverseInOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
        if (!root) return;
        for (const v of this.reverseInOrder(root.right!)) yield v;
        yield root.data;
        for (const v of this.reverseInOrder(root.left!)) yield v;
    }
}

class TreeSet<T = number> {
    _size: number;
    tree: RBTree<T>;
    compare: Compare<T>;
    constructor(
        collection: T[] | Compare<T> = [],
        compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0),
    ) {
        if (typeof collection === 'function') {
            compare = collection;
            collection = [];
        }
        this._size = 0;
        this.compare = compare;
        this.tree = new RBTree(compare);
        for (const val of collection) this.add(val);
    }

    size(): number {
        return this._size;
    }

    has(val: T): boolean {
        return !!this.tree.find(val);
    }

    add(val: T): boolean {
        const successful = this.tree.insert(val);
        this._size += successful ? 1 : 0;
        return successful;
    }

    delete(val: T): boolean {
        const deleted = this.tree.deleteAll(val);
        this._size -= deleted ? 1 : 0;
        return deleted;
    }

    ceil(val: T): T | undefined {
        let p = this.tree.root;
        let higher = null;
        while (p) {
            if (this.compare(p.data, val) >= 0) {
                higher = p;
                p = p.left;
            } else {
                p = p.right;
            }
        }
        return higher?.data;
    }

    floor(val: T): T | undefined {
        let p = this.tree.root;
        let lower = null;
        while (p) {
            if (this.compare(val, p.data) >= 0) {
                lower = p;
                p = p.right;
            } else {
                p = p.left;
            }
        }
        return lower?.data;
    }

    higher(val: T): T | undefined {
        let p = this.tree.root;
        let higher = null;
        while (p) {
            if (this.compare(val, p.data) < 0) {
                higher = p;
                p = p.left;
            } else {
                p = p.right;
            }
        }
        return higher?.data;
    }

    lower(val: T): T | undefined {
        let p = this.tree.root;
        let lower = null;
        while (p) {
            if (this.compare(p.data, val) < 0) {
                lower = p;
                p = p.right;
            } else {
                p = p.left;
            }
        }
        return lower?.data;
    }

    first(): T | undefined {
        return this.tree.inOrder().next().value;
    }

    last(): T | undefined {
        return this.tree.reverseInOrder().next().value;
    }

    shift(): T | undefined {
        const first = this.first();
        if (first === undefined) return undefined;
        this.delete(first);
        return first;
    }

    pop(): T | undefined {
        const last = this.last();
        if (last === undefined) return undefined;
        this.delete(last);
        return last;
    }

    *[Symbol.iterator](): Generator<T, void, void> {
        for (const val of this.values()) yield val;
    }

    *keys(): Generator<T, void, void> {
        for (const val of this.values()) yield val;
    }

    *values(): Generator<T, undefined, void> {
        for (const val of this.tree.inOrder()) yield val;
        return undefined;
    }

    /**
     * Return a generator for reverse order traversing the set
     */
    *rvalues(): Generator<T, undefined, void> {
        for (const val of this.tree.reverseInOrder()) yield val;
        return undefined;
    }
}

class TreeMultiSet<T = number> {
    _size: number;
    tree: RBTree<T>;
    compare: Compare<T>;
    constructor(
        collection: T[] | Compare<T> = [],
        compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0),
    ) {
        if (typeof collection === 'function') {
            compare = collection;
            collection = [];
        }
        this._size = 0;
        this.compare = compare;
        this.tree = new RBTree(compare);
        for (const val of collection) this.add(val);
    }

    size(): number {
        return this._size;
    }

    has(val: T): boolean {
        return !!this.tree.find(val);
    }

    add(val: T): boolean {
        const successful = this.tree.insert(val);
        this._size++;
        return successful;
    }

    delete(val: T): boolean {
        const successful = this.tree.delete(val);
        if (!successful) return false;
        this._size--;
        return true;
    }

    count(val: T): number {
        const node = this.tree.find(val);
        return node ? node.count : 0;
    }

    ceil(val: T): T | undefined {
        let p = this.tree.root;
        let higher = null;
        while (p) {
            if (this.compare(p.data, val) >= 0) {
                higher = p;
                p = p.left;
            } else {
                p = p.right;
            }
        }
        return higher?.data;
    }

    floor(val: T): T | undefined {
        let p = this.tree.root;
        let lower = null;
        while (p) {
            if (this.compare(val, p.data) >= 0) {
                lower = p;
                p = p.right;
            } else {
                p = p.left;
            }
        }
        return lower?.data;
    }

    higher(val: T): T | undefined {
        let p = this.tree.root;
        let higher = null;
        while (p) {
            if (this.compare(val, p.data) < 0) {
                higher = p;
                p = p.left;
            } else {
                p = p.right;
            }
        }
        return higher?.data;
    }

    lower(val: T): T | undefined {
        let p = this.tree.root;
        let lower = null;
        while (p) {
            if (this.compare(p.data, val) < 0) {
                lower = p;
                p = p.right;
            } else {
                p = p.left;
            }
        }
        return lower?.data;
    }

    first(): T | undefined {
        return this.tree.inOrder().next().value;
    }

    last(): T | undefined {
        return this.tree.reverseInOrder().next().value;
    }

    shift(): T | undefined {
        const first = this.first();
        if (first === undefined) return undefined;
        this.delete(first);
        return first;
    }

    pop(): T | undefined {
        const last = this.last();
        if (last === undefined) return undefined;
        this.delete(last);
        return last;
    }

    *[Symbol.iterator](): Generator<T, void, void> {
        yield* this.values();
    }

    *keys(): Generator<T, void, void> {
        for (const val of this.values()) yield val;
    }

    *values(): Generator<T, undefined, void> {
        for (const val of this.tree.inOrder()) {
            let count = this.count(val);
            while (count--) yield val;
        }
        return undefined;
    }

    /**
     * Return a generator for reverse order traversing the multi-set
     */
    *rvalues(): Generator<T, undefined, void> {
        for (const val of this.tree.reverseInOrder()) {
            let count = this.count(val);
            while (count--) yield val;
        }
        return undefined;
    }
}

1878 - Get Biggest Three Rhombus Sums in a Grid

1878. Get Biggest Three Rhombus Sums in a Grid

Level

Description

Solution

All Problems

All Solutions

Welcome to Subscribe On Youtube

1878. Get Biggest Three Rhombus Sums in a Grid

Level

Description

Solution

All Problems

All Solutions