Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1857.html
1857. Largest Color Value in a Directed Graph
Level
Hard
Description
There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.
You are given a string colors where colors[i] is a lowercase English letter representing the color of the i-th node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [a_j, b_j] indicates that there is a directed edge from node a_j to node b_j.
A valid path in the graph is a sequence of nodes x_1 -> x_2 -> x_3 -> ... -> x_k such that there is a directed edge from x_i to x_(i+1) for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.
Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.
Example 1:
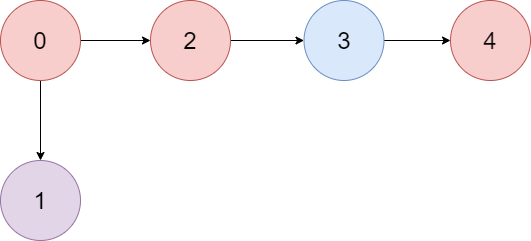
Input: colors = “abaca”, edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored “a” (red in the above image).
Example 2:
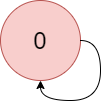
Input: colors = “a”, edges = [[0,0]]
Output: -1
Explanation: There is a cycle from 0 to 0.
Constraints:
n == colors.lengthm == edges.length1 <= n <= 10^50 <= m <= 10^5colorsconsists of lowercase English letters.0 <= a_j, b_j < n
Solution
Use topological sort and dynamic programming. Starting from all nodes with indegrees equal to 0, use topological sort to determine whether the graph contains a cycle. If the grapy contains a cycle, return -1. Otherwise, for each node, store the maximum frequency of each color. Maintain the maximum frequency during the process. Finally, return the maximum frequency.
-
class Solution { public int largestPathValue(String colors, int[][] edges) { int length = colors.length(); int[] indegrees = new int[length]; Map<Integer, List<Integer>> edgesMap = new HashMap<Integer, List<Integer>>(); for (int[] edge : edges) { int start = edge[0], end = edge[1]; indegrees[end]++; List<Integer> list = edgesMap.getOrDefault(start, new ArrayList<Integer>()); list.add(end); edgesMap.put(start, list); } int remain = length; Queue<Integer> queue = new LinkedList<Integer>(); for (int i = 0; i < length; i++) { if (indegrees[i] == 0) queue.offer(i); } int[][] dp = new int[length][26]; while (!queue.isEmpty()) { int node = queue.poll(); remain--; dp[node][colors.charAt(node) - 'a']++; List<Integer> list = edgesMap.getOrDefault(node, new ArrayList<Integer>()); for (int nextNode : list) { indegrees[nextNode]--; if (indegrees[nextNode] == 0) queue.offer(nextNode); for (int i = 0; i < 26; i++) dp[nextNode][i] = Math.max(dp[nextNode][i], dp[node][i]); } } if (remain > 0) return -1; int maxValue = 0; for (int i = 0; i < length; i++) maxValue = Math.max(maxValue, Arrays.stream(dp[i]).max().getAsInt()); return maxValue; } } ############ class Solution { public int largestPathValue(String colors, int[][] edges) { int n = colors.length(); List<Integer>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); int[] indeg = new int[n]; for (int[] e : edges) { int a = e[0], b = e[1]; g[a].add(b); ++indeg[b]; } Deque<Integer> q = new ArrayDeque<>(); int[][] dp = new int[n][26]; for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { q.offer(i); int c = colors.charAt(i) - 'a'; ++dp[i][c]; } } int cnt = 0; int ans = 1; while (!q.isEmpty()) { int i = q.pollFirst(); ++cnt; for (int j : g[i]) { if (--indeg[j] == 0) { q.offer(j); } int c = colors.charAt(j) - 'a'; for (int k = 0; k < 26; ++k) { dp[j][k] = Math.max(dp[j][k], dp[i][k] + (c == k ? 1 : 0)); ans = Math.max(ans, dp[j][k]); } } } return cnt == n ? ans : -1; } } -
class Solution: def largestPathValue(self, colors: str, edges: List[List[int]]) -> int: n = len(colors) indeg = [0] * n g = defaultdict(list) for a, b in edges: g[a].append(b) indeg[b] += 1 q = deque() dp = [[0] * 26 for _ in range(n)] for i, v in enumerate(indeg): if v == 0: q.append(i) c = ord(colors[i]) - ord('a') dp[i][c] += 1 cnt = 0 ans = 1 while q: i = q.popleft() cnt += 1 for j in g[i]: indeg[j] -= 1 if indeg[j] == 0: q.append(j) c = ord(colors[j]) - ord('a') for k in range(26): dp[j][k] = max(dp[j][k], dp[i][k] + (c == k)) ans = max(ans, dp[j][k]) return -1 if cnt < n else ans -
class Solution { public: int largestPathValue(string colors, vector<vector<int>>& edges) { int n = colors.size(); vector<vector<int>> g(n); vector<int> indeg(n); for (auto& e : edges) { int a = e[0], b = e[1]; g[a].push_back(b); ++indeg[b]; } queue<int> q; vector<vector<int>> dp(n, vector<int>(26)); for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { q.push(i); int c = colors[i] - 'a'; dp[i][c]++; } } int cnt = 0; int ans = 1; while (!q.empty()) { int i = q.front(); q.pop(); ++cnt; for (int j : g[i]) { if (--indeg[j] == 0) q.push(j); int c = colors[j] - 'a'; for (int k = 0; k < 26; ++k) { dp[j][k] = max(dp[j][k], dp[i][k] + (c == k)); ans = max(ans, dp[j][k]); } } } return cnt == n ? ans : -1; } }; -
func largestPathValue(colors string, edges [][]int) int { n := len(colors) g := make([][]int, n) indeg := make([]int, n) for _, e := range edges { a, b := e[0], e[1] g[a] = append(g[a], b) indeg[b]++ } q := []int{} dp := make([][]int, n) for i := range dp { dp[i] = make([]int, 26) } for i, v := range indeg { if v == 0 { q = append(q, i) c := colors[i] - 'a' dp[i][c]++ } } cnt := 0 ans := 1 for len(q) > 0 { i := q[0] q = q[1:] cnt++ for _, j := range g[i] { indeg[j]-- if indeg[j] == 0 { q = append(q, j) } c := int(colors[j] - 'a') for k := 0; k < 26; k++ { t := 0 if c == k { t = 1 } dp[j][k] = max(dp[j][k], dp[i][k]+t) ans = max(ans, dp[j][k]) } } } if cnt == n { return ans } return -1 } func max(a, b int) int { if a > b { return a } return b }