Welcome to Subscribe On Youtube
2050. Parallel Courses III
Description
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.
You must find the minimum number of months needed to complete all the courses following these rules:
- You may start taking a course at any time if the prerequisites are met.
- Any number of courses can be taken at the same time.
Return the minimum number of months needed to complete all the courses.
Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5] Output: 8 Explanation: The figure above represents the given graph and the time required to complete each course. We start course 1 and course 2 simultaneously at month 0. Course 1 takes 3 months and course 2 takes 2 months to complete respectively. Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
Example 2:
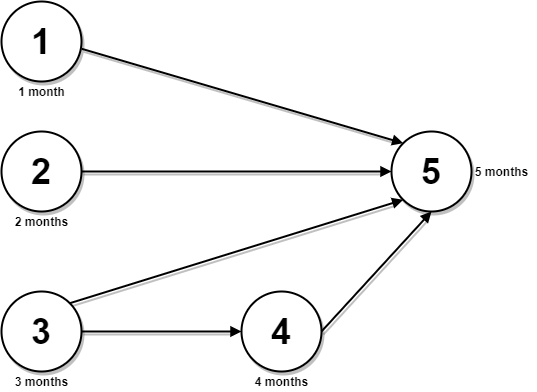
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5] Output: 12 Explanation: The figure above represents the given graph and the time required to complete each course. You can start courses 1, 2, and 3 at month 0. You can complete them after 1, 2, and 3 months respectively. Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months. Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months. Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
Constraints:
1 <= n <= 5 * 1040 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)relations[j].length == 21 <= prevCoursej, nextCoursej <= nprevCoursej != nextCoursej- All the pairs
[prevCoursej, nextCoursej]are unique. time.length == n1 <= time[i] <= 104- The given graph is a directed acyclic graph.
Solutions
-
class Solution { public int minimumTime(int n, int[][] relations, int[] time) { List<Integer>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); int[] indeg = new int[n]; for (int[] e : relations) { int a = e[0] - 1, b = e[1] - 1; g[a].add(b); ++indeg[b]; } Deque<Integer> q = new ArrayDeque<>(); int[] f = new int[n]; int ans = 0; for (int i = 0; i < n; ++i) { int v = indeg[i], t = time[i]; if (v == 0) { q.offer(i); f[i] = t; ans = Math.max(ans, t); } } while (!q.isEmpty()) { int i = q.pollFirst(); for (int j : g[i]) { f[j] = Math.max(f[j], f[i] + time[j]); ans = Math.max(ans, f[j]); if (--indeg[j] == 0) { q.offer(j); } } } return ans; } } -
class Solution { public: int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) { vector<vector<int>> g(n); vector<int> indeg(n); for (auto& e : relations) { int a = e[0] - 1, b = e[1] - 1; g[a].push_back(b); ++indeg[b]; } queue<int> q; vector<int> f(n); int ans = 0; for (int i = 0; i < n; ++i) { int v = indeg[i], t = time[i]; if (v == 0) { q.push(i); f[i] = t; ans = max(ans, t); } } while (!q.empty()) { int i = q.front(); q.pop(); for (int j : g[i]) { if (--indeg[j] == 0) { q.push(j); } f[j] = max(f[j], f[i] + time[j]); ans = max(ans, f[j]); } } return ans; } }; -
class Solution: def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int: g = defaultdict(list) indeg = [0] * n for a, b in relations: g[a - 1].append(b - 1) indeg[b - 1] += 1 q = deque() f = [0] * n ans = 0 for i, (v, t) in enumerate(zip(indeg, time)): if v == 0: q.append(i) f[i] = t ans = max(ans, t) while q: i = q.popleft() for j in g[i]: f[j] = max(f[j], f[i] + time[j]) ans = max(ans, f[j]) indeg[j] -= 1 if indeg[j] == 0: q.append(j) return ans -
func minimumTime(n int, relations [][]int, time []int) int { g := make([][]int, n) indeg := make([]int, n) for _, e := range relations { a, b := e[0]-1, e[1]-1 g[a] = append(g[a], b) indeg[b]++ } f := make([]int, n) q := []int{} ans := 0 for i, v := range indeg { if v == 0 { q = append(q, i) f[i] = time[i] ans = max(ans, time[i]) } } for len(q) > 0 { i := q[0] q = q[1:] for _, j := range g[i] { indeg[j]-- if indeg[j] == 0 { q = append(q, j) } f[j] = max(f[j], f[i]+time[j]) ans = max(ans, f[j]) } } return ans } -
function minimumTime(n: number, relations: number[][], time: number[]): number { const g: number[][] = Array(n) .fill(0) .map(() => []); const indeg: number[] = Array(n).fill(0); for (const [a, b] of relations) { g[a - 1].push(b - 1); ++indeg[b - 1]; } const q: number[] = []; const f: number[] = Array(n).fill(0); let ans: number = 0; for (let i = 0; i < n; ++i) { if (indeg[i] === 0) { q.push(i); f[i] = time[i]; ans = Math.max(ans, f[i]); } } while (q.length > 0) { const i = q.shift()!; for (const j of g[i]) { f[j] = Math.max(f[j], f[i] + time[j]); ans = Math.max(ans, f[j]); if (--indeg[j] === 0) { q.push(j); } } } return ans; }