Formatted question description: https://leetcode.ca/all/1840.html

1840. Maximum Building Height

Level

Hard

Description

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

The height of each building must be a non-negative integer.
The height of the first building must be 0.
The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [id_i, maxHeight_i] indicates that building id_i must have a height less than or equal to maxHeight_i.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

Example 1:

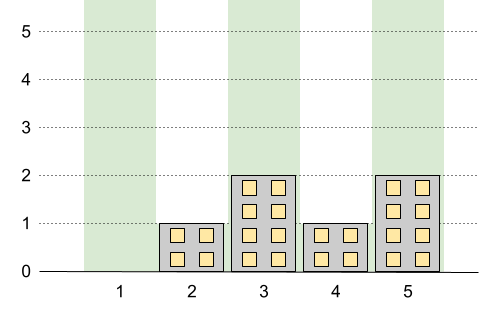
Image text

Input: n = 5, restrictions = [[2,1],[4,1]]

Output: 2

Explanation: The green area in the image indicates the maximum allowed height for each building.

We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

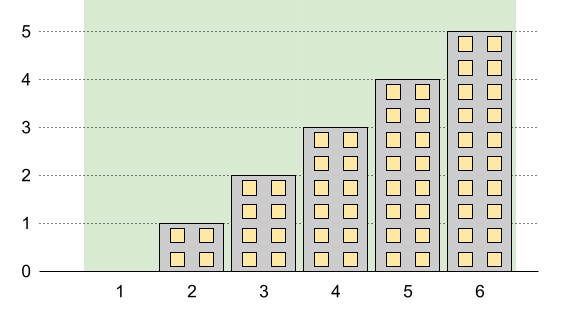
Image text

Input: n = 6, restrictions = []

Output: 5

Explanation: The green area in the image indicates the maximum allowed height for each building.

We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

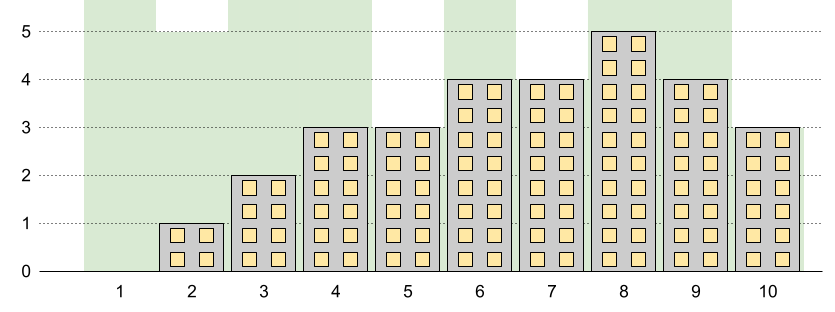
Image text

Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]

Output: 5

Explanation: The green area in the image indicates the maximum allowed height for each building.

We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

Constraints:

2 <= n <= 10^9
0 <= restrictions.length <= min(n - 1, 10^5)
2 <= id_i <= n
id_i is unique.
0 <= maxHeight_i <= 10^9

Solution

Sort restrictions according to the id values. Then loop over restrictions forward and backward to determine the actual maximum possible height of each element in restrictions. Next, for two adjacent restrictions [i, a] and [j, b] where i < j, the maximum possible height in the ranges [i, j] is (j - i + Math.abs(b - a)) / 2 + Math.min(a, b). The last thing is to calculate the maximum possible height of the building with id = n. Finally, return the maximum possible height among all n buildings.

class Solution {
    public int maxBuilding(int n, int[][] restrictions) {
        Arrays.sort(restrictions, new Comparator<int[]>() {
            public int compare(int[] restriction1, int[] restriction2) {
                return restriction1[0] - restriction2[0];
            }
        });
        int maxHeight = 0;
        int length = restrictions.length;
        int prevId = 1, prevHeight = 0;
        for (int i = 0; i < length; i++) {
            int[] restriction = restrictions[i];
            int currId = restriction[0], currHeight = restriction[1];
            int difference = currId - prevId;
            restrictions[i][1] = Math.min(restrictions[i][1], prevHeight + difference);
            prevId = currId;
            prevHeight = restrictions[i][1];
        }
        for (int i = length - 2; i >= 0; i--) {
            int difference = restrictions[i + 1][0] - restrictions[i][0];
            restrictions[i][1] = Math.min(restrictions[i][1], restrictions[i + 1][1] + difference);
        }
        prevId = 1;
        prevHeight = 0;
        for (int i = 0; i < length; i++) {
            int[] restriction = restrictions[i];
            int currId = restriction[0], currHeight = restriction[1];
            int difference = currId - prevId;
            restrictions[i][1] = Math.min(restrictions[i][1], prevHeight + difference);
            int heightDifference = Math.abs(currHeight - prevHeight);
            int curMaxHeight = (difference + heightDifference) / 2 + Math.min(prevHeight, currHeight);
            maxHeight = Math.max(maxHeight, curMaxHeight);
            prevId = currId;
            prevHeight = currHeight;
        }
        int lastHeight = prevHeight + (n - prevId);
        maxHeight = Math.max(maxHeight, lastHeight);
        return maxHeight;
    }
}

############

class Solution {
    public int maxBuilding(int n, int[][] restrictions) {
        List<int[]> r = new ArrayList<>();
        r.addAll(Arrays.asList(restrictions));
        r.add(new int[] {1, 0});
        Collections.sort(r, (a, b) -> a[0] - b[0]);
        if (r.get(r.size() - 1)[0] != n) {
            r.add(new int[] {n, n - 1});
        }
        int m = r.size();
        for (int i = 1; i < m; ++i) {
            int[] a = r.get(i - 1), b = r.get(i);
            b[1] = Math.min(b[1], a[1] + b[0] - a[0]);
        }
        for (int i = m - 2; i > 0; --i) {
            int[] a = r.get(i), b = r.get(i + 1);
            a[1] = Math.min(a[1], b[1] + b[0] - a[0]);
        }
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            int[] a = r.get(i), b = r.get(i + 1);
            int t = (a[1] + b[1] + b[0] - a[0]) / 2;
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

// OJ: https://leetcode.com/problems/maximum-building-height/
// Time: O(RlogR)
// Space: O(R)
class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& A) {
        map<long, long> m{ {1,0} };
        for (auto &v : A) m[v[0]] = v[1];
        long ans = 0;
        for (auto it = next(begin(m)); it != end(m);) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            if (h2 >= h1 + x2 - x1) {
                it = m.erase(it);
            } else {
                it = next(it);
            }
        }
        for (auto it = prev(end(m)); it != begin(m);) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            if (h1 >= h2 + x2 - x1) {
                m.erase(prev(it));
            } else {
                it = prev(it);
            }
        }
        for (auto it = next(begin(m)); it != end(m); ++it) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            long x = (h2 - h1 + x1 + x2) / 2;
            ans = max(ans, h1 + x - x1);
        }
        auto [x, h] = *rbegin(m);
        ans = max(ans, h + n - x);
        return ans;
    }
};

class Solution:
    def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int:
        r = restrictions
        r.append([1, 0])
        r.sort()
        if r[-1][0] != n:
            r.append([n, n - 1])
        m = len(r)
        for i in range(1, m):
            r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0])
        for i in range(m - 2, 0, -1):
            r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0])
        ans = 0
        for i in range(m - 1):
            t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2
            ans = max(ans, t)
        return ans

func maxBuilding(n int, restrictions [][]int) (ans int) {
	r := restrictions
	r = append(r, []int{1, 0})
	sort.Slice(r, func(i, j int) bool { return r[i][0] < r[j][0] })
	if r[len(r)-1][0] != n {
		r = append(r, []int{n, n - 1})
	}
	m := len(r)
	for i := 1; i < m; i++ {
		r[i][1] = min(r[i][1], r[i-1][1]+r[i][0]-r[i-1][0])
	}
	for i := m - 2; i > 0; i-- {
		r[i][1] = min(r[i][1], r[i+1][1]+r[i+1][0]-r[i][0])
	}
	for i := 0; i < m-1; i++ {
		t := (r[i][1] + r[i+1][1] + r[i+1][0] - r[i][0]) / 2
		ans = max(ans, t)
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

1840 - Maximum Building Height

1840. Maximum Building Height

Level

Description

Solution

All Problems

All Solutions

Welcome to Subscribe On Youtube

1840. Maximum Building Height

Level

Description

Solution

All Problems

All Solutions