Welcome to Subscribe On Youtube
2035. Partition Array Into Two Arrays to Minimize Sum Difference
Description
You are given an integer array nums of 2 * n integers. You need to partition nums into two arrays of length n to minimize the absolute difference of the sums of the arrays. To partition nums, put each element of nums into one of the two arrays.
Return the minimum possible absolute difference.
Example 1:
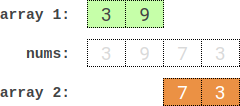
Input: nums = [3,9,7,3] Output: 2 Explanation: One optimal partition is: [3,9] and [7,3]. The absolute difference between the sums of the arrays is abs((3 + 9) - (7 + 3)) = 2.
Example 2:
Input: nums = [-36,36] Output: 72 Explanation: One optimal partition is: [-36] and [36]. The absolute difference between the sums of the arrays is abs((-36) - (36)) = 72.
Example 3:
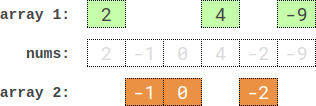
Input: nums = [2,-1,0,4,-2,-9] Output: 0 Explanation: One optimal partition is: [2,4,-9] and [-1,0,-2]. The absolute difference between the sums of the arrays is abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0.
Constraints:
1 <= n <= 15nums.length == 2 * n-107 <= nums[i] <= 107
Solutions
-
class Solution { public int minimumDifference(int[] nums) { int n = nums.length >> 1; Map<Integer, Set<Integer>> f = new HashMap<>(); Map<Integer, Set<Integer>> g = new HashMap<>(); for (int i = 0; i < (1 << n); ++i) { int s = 0, cnt = 0; int s1 = 0, cnt1 = 0; for (int j = 0; j < n; ++j) { if ((i & (1 << j)) != 0) { s += nums[j]; ++cnt; s1 += nums[n + j]; ++cnt1; } else { s -= nums[j]; s1 -= nums[n + j]; } } f.computeIfAbsent(cnt, k -> new HashSet<>()).add(s); g.computeIfAbsent(cnt1, k -> new HashSet<>()).add(s1); } int ans = Integer.MAX_VALUE; for (int i = 0; i <= n; ++i) { List<Integer> fi = new ArrayList<>(f.get(i)); List<Integer> gi = new ArrayList<>(g.get(n - i)); Collections.sort(fi); Collections.sort(gi); for (int a : fi) { int left = 0, right = gi.size() - 1; int b = -a; while (left < right) { int mid = (left + right) >> 1; if (gi.get(mid) >= b) { right = mid; } else { left = mid + 1; } } ans = Math.min(ans, Math.abs(a + gi.get(left))); if (left > 0) { ans = Math.min(ans, Math.abs(a + gi.get(left - 1))); } } } return ans; } } -
class Solution { public: int minimumDifference(vector<int>& nums) { int n = nums.size() >> 1; vector<vector<int>> f(n + 1), g(n + 1); for (int i = 0; i < (1 << n); ++i) { int s = 0, cnt = 0; int s1 = 0, cnt1 = 0; for (int j = 0; j < n; ++j) { if (i & (1 << j)) { s += nums[j]; ++cnt; s1 += nums[n + j]; ++cnt1; } else { s -= nums[j]; s1 -= nums[n + j]; } } f[cnt].push_back(s); g[cnt1].push_back(s1); } for (int i = 0; i <= n; ++i) { sort(f[i].begin(), f[i].end()); sort(g[i].begin(), g[i].end()); } int ans = INT_MAX; for (int i = 0; i <= n; ++i) { for (int a : f[i]) { int left = 0, right = g[n - i].size() - 1; int b = -a; while (left < right) { int mid = (left + right) >> 1; if (g[n - i][mid] >= b) right = mid; else left = mid + 1; } ans = min(ans, abs(a + g[n - i][left])); if (left > 0) ans = min(ans, abs(a + g[n - i][left - 1])); } } return ans; } }; -
class Solution: def minimumDifference(self, nums: List[int]) -> int: n = len(nums) >> 1 f = defaultdict(set) g = defaultdict(set) for i in range(1 << n): s = cnt = 0 s1 = cnt1 = 0 for j in range(n): if (i & (1 << j)) != 0: s += nums[j] cnt += 1 s1 += nums[n + j] cnt1 += 1 else: s -= nums[j] s1 -= nums[n + j] f[cnt].add(s) g[cnt1].add(s1) ans = inf for i in range(n + 1): fi, gi = sorted(list(f[i])), sorted(list(g[n - i])) # min(abs(f[i] + g[n - i])) for a in fi: left, right = 0, len(gi) - 1 b = -a while left < right: mid = (left + right) >> 1 if gi[mid] >= b: right = mid else: left = mid + 1 ans = min(ans, abs(a + gi[left])) if left > 0: ans = min(ans, abs(a + gi[left - 1])) return ans -
func minimumDifference(nums []int) int { n := len(nums) >> 1 f := make([][]int, n+1) g := make([][]int, n+1) for i := 0; i < (1 << n); i++ { s, cnt := 0, 0 s1, cnt1 := 0, 0 for j := 0; j < n; j++ { if (i & (1 << j)) != 0 { s += nums[j] cnt++ s1 += nums[n+j] cnt1++ } else { s -= nums[j] s1 -= nums[n+j] } } f[cnt] = append(f[cnt], s) g[cnt1] = append(g[cnt1], s1) } for i := 0; i <= n; i++ { sort.Ints(f[i]) sort.Ints(g[i]) } ans := 1 << 30 for i := 0; i <= n; i++ { for _, a := range f[i] { left, right := 0, len(g[n-i])-1 b := -a for left < right { mid := (left + right) >> 1 if g[n-i][mid] >= b { right = mid } else { left = mid + 1 } } ans = min(ans, abs(a+g[n-i][left])) if left > 0 { ans = min(ans, abs(a+g[n-i][left-1])) } } } return ans } func abs(x int) int { if x > 0 { return x } return -x }