Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1823.html
1823. Find the Winner of the Circular Game
Level
Medium
Description
There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the i-th friend brings you to the (i+1)-th friend for 1 <= i < n, and moving clockwise from the n-th friend brings you to the 1st friend.
The rules of the game are as follows:
- Start at the
1stfriend. - Count the next
kfriends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once. - The last friend you counted leaves the circle and loses the game.
- If there is still more than one friend in the circle, go back to step
2starting from the friend immediately clockwise of the friend who just lost and repeat. - Else, the last friend in the circle wins the game.
Given the number of friends, n, and an integer k, return the winner of the game.
Example 1:
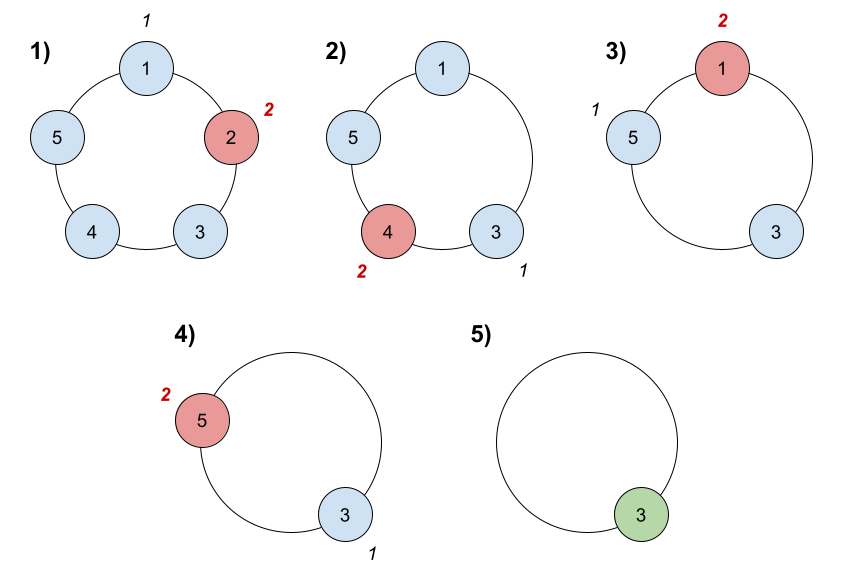
Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
Example 2:
Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
Constraints:
1 <= k <= n <= 500
Solution
This is the Josephus problem. Use the solution to the Josephus problem to solve this problem.
-
class Solution { public int findTheWinner(int n, int k) { int last = 0; for (int i = 2; i <= n; i++) last = (last + k) % i; last = last % n + 1; return last; } } ############ class Solution { public int findTheWinner(int n, int k) { if (n == 1) { return 1; } int ans = (findTheWinner(n - 1, k) + k) % n; return ans == 0 ? n : ans; } } -
// OJ: https://leetcode.com/problems/find-the-winner-of-the-circular-game/ // Time: O(NK) // Space: O(N) class Solution { public: int findTheWinner(int n, int k) { set<int> s; for (int i = 1; i <= n; ++i) { s.insert(i); } auto it = begin(s); while (s.size() > 1) { for (int i = 1; i < k; ++i) { it = it == prev(s.end()) ? begin(s) : next(it); } auto j = it == prev(s.end()) ? begin(s) : next(it); s.erase(it); it = j; } return *s.begin(); } }; -
class Solution: def findTheWinner(self, n: int, k: int) -> int: if n == 1: return 1 ans = (k + self.findTheWinner(n - 1, k)) % n return n if ans == 0 else ans ############ # 1823. Find the Winner of the Circular Game # https://leetcode.com/problems/find-the-winner-of-the-circular-game class Solution: def findTheWinner(self, n: int, k: int) -> int: A = [i for i in range(1, n + 1)] curr = 0 while len(A) > 1: remove = A[(curr + k - 1) % len(A)] curr = (curr + k - 1) % len(A) A = [x for x in A if x != remove] return A[0] -
func findTheWinner(n int, k int) int { if n == 1 { return 1 } ans := (findTheWinner(n-1, k) + k) % n if ans == 0 { return n } return ans } -
class LinkNode { public val: number; public next: LinkNode; constructor(val: number = 0, next?: LinkNode) { this.val = val; this.next = next; } } function findTheWinner(n: number, k: number): number { if (k === 1) { return n; } const dummy = new LinkNode(0); let cur = dummy; for (let i = 1; i <= n; i++) { cur.next = new LinkNode(i); cur = cur.next; } cur.next = dummy.next; cur = dummy; let count = 0; while (cur.next != cur) { count++; if (count === k) { cur.next = cur.next.next; count = 0; } else { cur = cur.next; } } return cur.val; }