Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1819.html

1819. Number of Different Subsequences GCDs

Level

Hard

Description

You are given an array nums that consists of positive integers.

The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly.

• For example, the GCD of the sequence [4,6,16] is 2.

A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.

• For example, [2,5,10] is a subsequence of [1,2,1,2,4,1,5,10].

Return the number of different GCDs among all non-empty subsequences of nums.

Example 1:

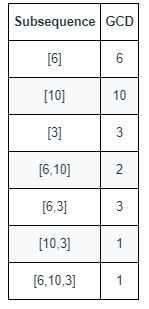
Input: nums = [6,10,3]

Output: 5

Explanation: The figure shows all the non-empty subsequences and their GCDs.

The different GCDs are 6, 10, 3, 2, and 1.

Example 2:

Input: nums = [5,15,40,5,6]

Output: 7

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 2 * 10^5

Solution

For each num in nums, obtain all the factors of num. Count the number of each factor from 1 to max(nums). For each i such that 1 <= i <= max(nums), let counts[i] be the number of factor i that occurs in nums. If i is in nums, or counts[i] > 0 and there does not exist any j such that j > i and j % i == 0, then i is the GCD of a subsequence of nums. Finally, return the number of different subsequences GCDs.

• Java
• C++
• Python
• Go

• class Solution {
      public int countDifferentSubsequenceGCDs(int[] nums) {
          Set<Integer> set = new HashSet<Integer>();
          int max = 0;
          for (int num : nums) {
              set.add(num);
              max = Math.max(max, num);
          }
          int[] counts = new int[max + 1];
          for (int num : set) {
              for (int i = 1; i * i <= num; i++) {
                  if (num % i == 0) {
                      counts[i]++;
                      if (i * i != num)
                          counts[num / i]++;
                  }
              }
          }
          int count = 0;
          for (int i = 1; i <= max; i++) {
              if (set.contains(i))
                  count++;
              else if (counts[i] > 0) {
                  boolean flag = true;
                  for (int j = i * 2; j <= max; j += i) {
                      if (counts[j] == counts[i]) {
                          flag = false;
                          break;
                      }
                  }
                  if (flag)
                      count++;
              }
          }
          return count;
      }
  }
  
  ############
  
  class Solution {
      public int countDifferentSubsequenceGCDs(int[] nums) {
          int mx = Arrays.stream(nums).max().getAsInt();
          boolean[] vis = new boolean[mx + 1];
          for (int x : nums) {
              vis[x] = true;
          }
          int ans = 0;
          for (int x = 1; x <= mx; ++x) {
              int g = 0;
              for (int y = x; y <= mx; y += x) {
                  if (vis[y]) {
                      g = gcd(g, y);
                      if (x == g) {
                          ++ans;
                          break;
                      }
                  }
              }
          }
          return ans;
      }
  
      private int gcd(int a, int b) {
          return b == 0 ? a : gcd(b, a % b);
      }
  }
  

• // OJ: https://leetcode.com/problems/number-of-different-subsequences-gcds/
  // Time: O(NlogN)
  // Space: O(N)
  class Solution {
  public:
      int countDifferentSubsequenceGCDs(vector<int>& A) {
          const int N = 2e5;
          int ans = 0;
          bool seen[N + 1] = {};
          for (int n : A) seen[n] = true;
          for (int i = 1; i <= N; ++i) {
              int div = 0;
              for (int j = i; j <= N; j += i) {
                  if (seen[j]) div = gcd(div, j);
              }
              if (div == i) ++ans;
          }
          return ans;
      }
  };
  

• class Solution:
      def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int:
          mx = max(nums)
          vis = set(nums)
          ans = 0
          for x in range(1, mx + 1):
              g = 0
              for y in range(x, mx + 1, x):
                  if y in vis:
                      g = gcd(g, y)
                      if g == x:
                          ans += 1
                          break
          return ans
  
  
  

• func countDifferentSubsequenceGCDs(nums []int) (ans int) {
  	mx := 0
  	for _, x := range nums {
  		mx = max(mx, x)
  	}
  	vis := make([]bool, mx+1)
  	for _, x := range nums {
  		vis[x] = true
  	}
  	for x := 1; x <= mx; x++ {
  		g := 0
  		for y := x; y <= mx; y += x {
  			if vis[y] {
  				g = gcd(g, y)
  				if g == x {
  					ans++
  					break
  				}
  			}
  		}
  	}
  	return
  }
  
  func max(a, b int) int {
  	if a > b {
  		return a
  	}
  	return b
  }
  
  func gcd(a, b int) int {
  	if b == 0 {
  		return a
  	}
  	return gcd(b, a%b)
  }
  

All Problems

All Solutions