Welcome to Subscribe On Youtube
2013. Detect Squares
Description
You are given a stream of points on the X-Y plane. Design an algorithm that:
- Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
- Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.
An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the DetectSquares class:
DetectSquares()Initializes the object with an empty data structure.void add(int[] point)Adds a new pointpoint = [x, y]to the data structure.int count(int[] point)Counts the number of ways to form axis-aligned squares with pointpoint = [x, y]as described above.
Example 1:
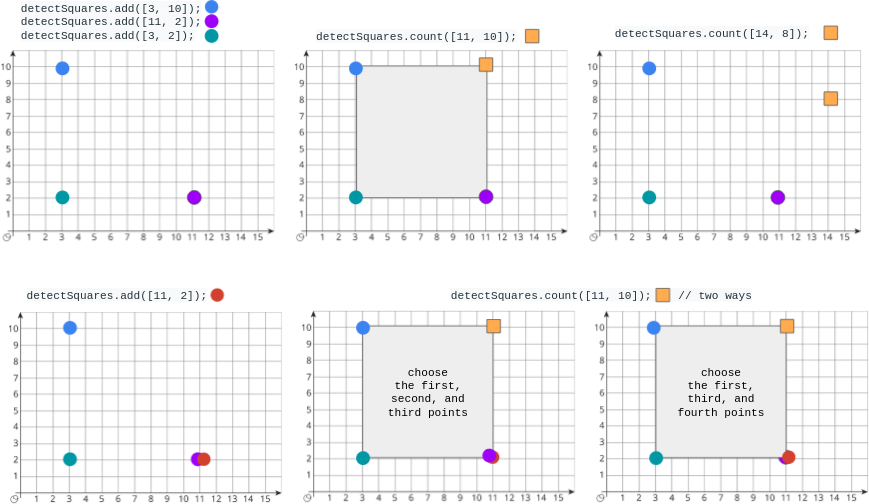
Input ["DetectSquares", "add", "add", "add", "count", "count", "add", "count"] [[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]] Output [null, null, null, null, 1, 0, null, 2] Explanation DetectSquares detectSquares = new DetectSquares(); detectSquares.add([3, 10]); detectSquares.add([11, 2]); detectSquares.add([3, 2]); detectSquares.count([11, 10]); // return 1. You can choose: // - The first, second, and third points detectSquares.count([14, 8]); // return 0. The query point cannot form a square with any points in the data structure. detectSquares.add([11, 2]); // Adding duplicate points is allowed. detectSquares.count([11, 10]); // return 2. You can choose: // - The first, second, and third points // - The first, third, and fourth points
Constraints:
point.length == 20 <= x, y <= 1000- At most
3000calls in total will be made toaddandcount.
Solutions
Solution 1: Hash Table
We can use a hash table $cnt$ to maintain all the information of the points, where $cnt[x][y]$ represents the count of point $(x, y)$.
When calling the $add(x, y)$ method, we increase the value of $cnt[x][y]$ by $1$.
When calling the $count(x_1, y_1)$ method, we need to get three other points to form an axis-aligned square. We can enumerate the point $(x_2, y_1)$ that is parallel to the $x$-axis and at a distance $d$ from $(x_1, y_1)$. If such a point exists, based on these two points, we can determine the other two points as $(x_1, y_1 + d)$ and $(x_2, y_1 + d)$, or $(x_1, y_1 - d)$ and $(x_2, y_1 - d)$. We can add up the number of schemes for these two situations.
In terms of time complexity, the time complexity of calling the $add(x, y)$ method is $O(1)$, and the time complexity of calling the $count(x_1, y_1)$ method is $O(n)$; the space complexity is $O(n)$. Here, $n$ is the number of points in the data stream.
-
class DetectSquares { private Map<Integer, Map<Integer, Integer>> cnt = new HashMap<>(); public DetectSquares() { } public void add(int[] point) { int x = point[0], y = point[1]; cnt.computeIfAbsent(x, k -> new HashMap<>()).merge(y, 1, Integer::sum); } public int count(int[] point) { int x1 = point[0], y1 = point[1]; if (!cnt.containsKey(x1)) { return 0; } int ans = 0; for (var e : cnt.entrySet()) { int x2 = e.getKey(); if (x2 != x1) { int d = x2 - x1; var cnt1 = cnt.get(x1); var cnt2 = e.getValue(); ans += cnt2.getOrDefault(y1, 0) * cnt1.getOrDefault(y1 + d, 0) * cnt2.getOrDefault(y1 + d, 0); ans += cnt2.getOrDefault(y1, 0) * cnt1.getOrDefault(y1 - d, 0) * cnt2.getOrDefault(y1 - d, 0); } } return ans; } } /** * Your DetectSquares object will be instantiated and called as such: * DetectSquares obj = new DetectSquares(); * obj.add(point); * int param_2 = obj.count(point); */ -
class DetectSquares { public: DetectSquares() { } void add(vector<int> point) { int x = point[0], y = point[1]; ++cnt[x][y]; } int count(vector<int> point) { int x1 = point[0], y1 = point[1]; if (!cnt.count(x1)) { return 0; } int ans = 0; for (auto& [x2, cnt2] : cnt) { if (x2 != x1) { int d = x2 - x1; auto& cnt1 = cnt[x1]; ans += cnt2[y1] * cnt1[y1 + d] * cnt2[y1 + d]; ans += cnt2[y1] * cnt1[y1 - d] * cnt2[y1 - d]; } } return ans; } private: unordered_map<int, unordered_map<int, int>> cnt; }; /** * Your DetectSquares object will be instantiated and called as such: * DetectSquares* obj = new DetectSquares(); * obj->add(point); * int param_2 = obj->count(point); */ -
class DetectSquares: def __init__(self): self.cnt = defaultdict(Counter) def add(self, point: List[int]) -> None: x, y = point self.cnt[x][y] += 1 def count(self, point: List[int]) -> int: x1, y1 = point if x1 not in self.cnt: return 0 ans = 0 for x2 in self.cnt.keys(): if x2 != x1: d = x2 - x1 ans += self.cnt[x2][y1] * self.cnt[x1][y1 + d] * self.cnt[x2][y1 + d] ans += self.cnt[x2][y1] * self.cnt[x1][y1 - d] * self.cnt[x2][y1 - d] return ans # Your DetectSquares object will be instantiated and called as such: # obj = DetectSquares() # obj.add(point) # param_2 = obj.count(point) -
type DetectSquares struct { cnt map[int]map[int]int } func Constructor() DetectSquares { return DetectSquares{map[int]map[int]int{} } } func (this *DetectSquares) Add(point []int) { x, y := point[0], point[1] if _, ok := this.cnt[x]; !ok { this.cnt[x] = map[int]int{} } this.cnt[x][y]++ } func (this *DetectSquares) Count(point []int) (ans int) { x1, y1 := point[0], point[1] if cnt1, ok := this.cnt[x1]; ok { for x2, cnt2 := range this.cnt { if x2 != x1 { d := x2 - x1 ans += cnt2[y1] * cnt1[y1+d] * cnt2[y1+d] ans += cnt2[y1] * cnt1[y1-d] * cnt2[y1-d] } } } return } /** * Your DetectSquares object will be instantiated and called as such: * obj := Constructor(); * obj.Add(point); * param_2 := obj.Count(point); */