Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1782.html
1782. Count Pairs Of Nodes
Level
Hard
Description
You are given an undirected graph represented by an integer n, which is the number of nodes, and edges, where edges[i] = [u_i, v_i] which indicates that there is an undirected edge between u_i and v_i. You are also given an integer array queries.
The answer to the j-th query is the number of pairs of nodes (a, b) that satisfy the following conditions:
a < bcntis strictly greater thanqueries[j], wherecntis the number of edges incident toaorb.
Return an array answers such that answers.length == queries.length and answers[j] is the answer of the j-th query.
Note that there can be repeated edges.
Example 1:
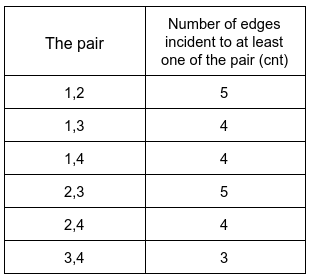
Input: n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
Output: [6,5]
Explanation: The number of edges incident to at least one of each pair is shown above.
Example 2:
Input: n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
Output: [10,10,9,8,6]
Constraints:
2 <= n <= 2 * 10^41 <= edges.length <= 10^51 <= u_i, v_i <= nu_i != v_i1 <= queries.length <= 200 <= queries[j] < edges.length
Solution
First, calculate the degrees of each node and the counts of each edge. Next, use another array arr to store the degrees and sort arr. Then, for each query, use two pointers to calculate the number of pairs of nodes that satisfy the conditions. Finally, return the query result.
-
class Solution { public int[] countPairs(int n, int[][] edges, int[] queries) { final int FACTOR = 100000; int[] degrees = new int[n + 1]; int[] arr = new int[n + 1]; int length = queries.length; int[] pairs = new int[length]; Map<Integer, Integer> map = new HashMap<Integer, Integer>(); for (int[] edge : edges) { int u = Math.min(edge[0], edge[1]); int v = Math.max(edge[0], edge[1]); degrees[u]++; degrees[v]++; int key = u * FACTOR + v; map.put(key, map.getOrDefault(key, 0) + 1); } for (int i = 1; i <= n; i++) arr[i] = degrees[i]; Arrays.sort(arr); for (int i = 0; i < length; i++) { int low = 1, high = n; while (low < high) { while (low < high && arr[low] + arr[high] <= queries[i]) low++; if (low < high) pairs[i] += high - low; high--; } if (pairs[i] != 0) { Set<Integer> visited = new HashSet<Integer>(); for (int[] edge : edges) { int u = Math.min(edge[0], edge[1]); int v = Math.max(edge[0], edge[1]); int key = u * FACTOR + v; if (visited.add(key)) { int pair = degrees[u] + degrees[v] - map.get(key); if (degrees[u] + degrees[v] > queries[i] && pair <= queries[i]) pairs[i]--; } } } } return pairs; } } ############ class Solution { public int[] countPairs(int n, int[][] edges, int[] queries) { int[] cnt = new int[n]; Map<Integer, Integer> g = new HashMap<>(); for (var e : edges) { int a = e[0] - 1, b = e[1] - 1; ++cnt[a]; ++cnt[b]; int k = Math.min(a, b) * n + Math.max(a, b); g.put(k, g.getOrDefault(k, 0) + 1); } int[] s = cnt.clone(); Arrays.sort(s); int[] ans = new int[queries.length]; for (int i = 0; i < queries.length; ++i) { int t = queries[i]; for (int j = 0; j < n; ++j) { int x = s[j]; int k = search(s, t - x, j + 1); ans[i] += n - k; } for (var e : g.entrySet()) { int a = e.getKey() / n, b = e.getKey() % n; int v = e.getValue(); if (cnt[a] + cnt[b] > t && cnt[a] + cnt[b] - v <= t) { --ans[i]; } } } return ans; } private int search(int[] arr, int x, int i) { int left = i, right = arr.length; while (left < right) { int mid = (left + right) >> 1; if (arr[mid] > x) { right = mid; } else { left = mid + 1; } } return left; } } -
class Solution: def countPairs( self, n: int, edges: List[List[int]], queries: List[int] ) -> List[int]: cnt = [0] * n g = defaultdict(int) for a, b in edges: a, b = a - 1, b - 1 cnt[a] += 1 cnt[b] += 1 if a > b: a, b = b, a g[(a, b)] += 1 s = sorted(cnt) ans = [0] * len(queries) for i, t in enumerate(queries): for j, x in enumerate(s): k = bisect_right(s, t - x, lo=j + 1) ans[i] += n - k for (a, b), v in g.items(): if cnt[a] + cnt[b] > t and cnt[a] + cnt[b] - v <= t: ans[i] -= 1 return ans -
class Solution { public: vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) { vector<int> cnt(n); unordered_map<int, int> g; for (auto& e : edges) { int a = e[0] - 1, b = e[1] - 1; ++cnt[a]; ++cnt[b]; int k = min(a, b) * n + max(a, b); ++g[k]; } vector<int> s = cnt; sort(s.begin(), s.end()); vector<int> ans(queries.size()); for (int i = 0; i < queries.size(); ++i) { int t = queries[i]; for (int j = 0; j < n; ++j) { int x = s[j]; int k = upper_bound(s.begin() + j + 1, s.end(), t - x) - s.begin(); ans[i] += n - k; } for (auto& [k, v] : g) { int a = k / n, b = k % n; if (cnt[a] + cnt[b] > t && cnt[a] + cnt[b] - v <= t) { --ans[i]; } } } return ans; } }; -
func countPairs(n int, edges [][]int, queries []int) []int { cnt := make([]int, n) g := map[int]int{} for _, e := range edges { a, b := e[0]-1, e[1]-1 cnt[a]++ cnt[b]++ if a > b { a, b = b, a } g[a*n+b]++ } s := make([]int, n) copy(s, cnt) sort.Ints(s) ans := make([]int, len(queries)) for i, t := range queries { for j, x := range s { k := sort.Search(n, func(h int) bool { return s[h] > t-x && h > j }) ans[i] += n - k } for k, v := range g { a, b := k/n, k%n if cnt[a]+cnt[b] > t && cnt[a]+cnt[b]-v <= t { ans[i]-- } } } return ans } -
function countPairs(n: number, edges: number[][], queries: number[]): number[] { const cnt: number[] = new Array(n).fill(0); const g: Map<number, number> = new Map(); for (const [a, b] of edges) { ++cnt[a - 1]; ++cnt[b - 1]; const k = Math.min(a - 1, b - 1) * n + Math.max(a - 1, b - 1); g.set(k, (g.get(k) || 0) + 1); } const s = cnt.slice().sort((a, b) => a - b); const search = (nums: number[], x: number, l: number): number => { let r = nums.length; while (l < r) { const mid = (l + r) >> 1; if (nums[mid] > x) { r = mid; } else { l = mid + 1; } } return l; }; const ans: number[] = []; for (const t of queries) { let res = 0; for (let j = 0; j < s.length; ++j) { const k = search(s, t - s[j], j + 1); res += n - k; } for (const [k, v] of g) { const a = Math.floor(k / n); const b = k % n; if (cnt[a] + cnt[b] > t && cnt[a] + cnt[b] - v <= t) { --res; } } ans.push(res); } return ans; }