Welcome to Subscribe On Youtube

1975. Maximum Matrix Sum

Description

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.

 

Example 1:

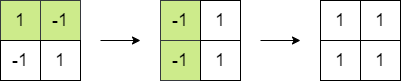
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

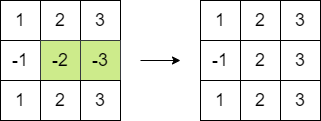
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

 

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

Solutions

• Java
• C++
• Python
• Go
• Javascript

• class Solution {
      public long maxMatrixSum(int[][] matrix) {
          long s = 0;
          int cnt = 0;
          int mi = Integer.MAX_VALUE;
          for (var row : matrix) {
              for (var v : row) {
                  s += Math.abs(v);
                  mi = Math.min(mi, Math.abs(v));
                  if (v < 0) {
                      ++cnt;
                  }
              }
          }
          if (cnt % 2 == 0 || mi == 0) {
              return s;
          }
          return s - mi * 2;
      }
  }
  

• class Solution {
  public:
      long long maxMatrixSum(vector<vector<int>>& matrix) {
          long long s = 0;
          int cnt = 0, mi = INT_MAX;
          for (auto& row : matrix) {
              for (int& v : row) {
                  s += abs(v);
                  mi = min(mi, abs(v));
                  cnt += v < 0;
              }
          }
          if (cnt % 2 == 0 || mi == 0) return s;
          return s - mi * 2;
      }
  };
  

• class Solution:
      def maxMatrixSum(self, matrix: List[List[int]]) -> int:
          s = cnt = 0
          mi = inf
          for row in matrix:
              for v in row:
                  s += abs(v)
                  mi = min(mi, abs(v))
                  if v < 0:
                      cnt += 1
          if cnt % 2 == 0 or mi == 0:
              return s
          return s - mi * 2
  
  

• func maxMatrixSum(matrix [][]int) int64 {
  	s := 0
  	cnt, mi := 0, math.MaxInt32
  	for _, row := range matrix {
  		for _, v := range row {
  			s += abs(v)
  			mi = min(mi, abs(v))
  			if v < 0 {
  				cnt++
  			}
  		}
  	}
  	if cnt%2 == 1 {
  		s -= mi * 2
  	}
  	return int64(s)
  }
  
  func abs(x int) int {
  	if x < 0 {
  		return -x
  	}
  	return x
  }
  

• /**
   * @param {number[][]} matrix
   * @return {number}
   */
  var maxMatrixSum = function (matrix) {
      let cnt = 0;
      let s = 0;
      let mi = Infinity;
      for (const row of matrix) {
          for (const v of row) {
              s += Math.abs(v);
              mi = Math.min(mi, Math.abs(v));
              cnt += v < 0;
          }
      }
      if (cnt % 2 == 0) {
          return s;
      }
      return s - mi * 2;
  };
  
  

All Problems

All Solutions