Welcome to Subscribe On Youtube
1954. Minimum Garden Perimeter to Collect Enough Apples
Description
In a garden represented as an infinite 2D grid, there is an apple tree planted at every integer coordinate. The apple tree planted at an integer coordinate (i, j) has |i| + |j| apples growing on it.
You will buy an axis-aligned square plot of land that is centered at (0, 0).
Given an integer neededApples, return the minimum perimeter of a plot such that at least neededApples apples are inside or on the perimeter of that plot.
The value of |x| is defined as:
xifx >= 0-xifx < 0
Example 1:
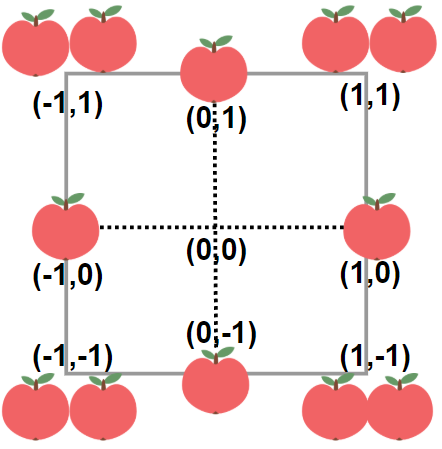
Input: neededApples = 1 Output: 8 Explanation: A square plot of side length 1 does not contain any apples. However, a square plot of side length 2 has 12 apples inside (as depicted in the image above). The perimeter is 2 * 4 = 8.
Example 2:
Input: neededApples = 13 Output: 16
Example 3:
Input: neededApples = 1000000000 Output: 5040
Constraints:
1 <= neededApples <= 1015
Solutions
-
class Solution { public long minimumPerimeter(long neededApples) { long x = 1; while (2 * x * (x + 1) * (2 * x + 1) < neededApples) { ++x; } return 8 * x; } } -
class Solution { public: long long minimumPerimeter(long long neededApples) { long long x = 1; while (2 * x * (x + 1) * (2 * x + 1) < neededApples) { ++x; } return 8 * x; } }; -
class Solution: def minimumPerimeter(self, neededApples: int) -> int: x = 1 while 2 * x * (x + 1) * (2 * x + 1) < neededApples: x += 1 return x * 8 -
func minimumPerimeter(neededApples int64) int64 { var x int64 = 1 for 2*x*(x+1)*(2*x+1) < neededApples { x++ } return 8 * x } -
function minimumPerimeter(neededApples: number): number { let x = 1; while (2 * x * (x + 1) * (2 * x + 1) < neededApples) { ++x; } return 8 * x; }