Welcome to Subscribe On Youtube
1938. Maximum Genetic Difference Query
Description
There is a rooted tree consisting of n nodes numbered 0 to n - 1. Each node's number denotes its unique genetic value (i.e. the genetic value of node x is x). The genetic difference between two genetic values is defined as the bitwise-XOR of their values. You are given the integer array parents, where parents[i] is the parent for node i. If node x is the root of the tree, then parents[x] == -1.
You are also given the array queries where queries[i] = [nodei, vali]. For each query i, find the maximum genetic difference between vali and pi, where pi is the genetic value of any node that is on the path between nodei and the root (including nodei and the root). More formally, you want to maximize vali XOR pi.
Return an array ans where ans[i] is the answer to the ith query.
Example 1:
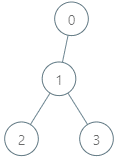
Input: parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]] Output: [2,3,7] Explanation: The queries are processed as follows: - [0,2]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2. - [3,2]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3. - [2,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
Example 2:
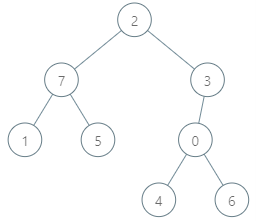
Input: parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]] Output: [6,14,7] Explanation: The queries are processed as follows: - [4,6]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6. - [1,15]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14. - [0,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
Constraints:
2 <= parents.length <= 1050 <= parents[i] <= parents.length - 1for every nodeithat is not the root.parents[root] == -11 <= queries.length <= 3 * 1040 <= nodei <= parents.length - 10 <= vali <= 2 * 105
Solution
Create a trie that stores the numbers in nums. Each node in the trie has two children that represent bits 0 and 1, respectively. For each number, create the trie from the highest bit to the lowest bit, where all the numbers have at most 18 bits. For each node in the trie, maintain the number of times that the node is passed by.
Then do depth first search on the trie starting from the root to obtain the query results.
Finally, return the query results.
-
class Solution { static final int MAXD = 17; public int[] maxGeneticDifference(int[] parents, int[][] queries) { int n = parents.length; List<List<Integer>> edges = new ArrayList<List<Integer>>(); for (int i = 0; i < n; i++) edges.add(new ArrayList<Integer>()); int rootIndex = -1; for (int i = 0; i < n; i++) { if (parents[i] == -1) rootIndex = i; else edges.get(parents[i]).add(i); } List<List<int[]>> stored = new ArrayList<List<int[]>>(); for (int i = 0; i < n; i++) stored.add(new ArrayList<int[]>()); int queriesCount = queries.length; int[] ans = new int[queriesCount]; for (int i = 0; i < queriesCount; i++) stored.get(queries[i][0]).add(new int[]{i, queries[i][1]}); TrieNode root = new TrieNode(); depthFirstSearch(ans, root, rootIndex, edges, stored); return ans; } public void insert(TrieNode root, int x) { TrieNode curr = root; for (int i = MAXD; i >= 0; i--) { if ((x & (1 << i)) != 0) { if (curr.children[1] == null) curr.children[1] = new TrieNode(); curr = curr.children[1]; } else { if (curr.children[0] == null) curr.children[0] = new TrieNode(); curr = curr.children[0]; } curr.count++; } } public int query(TrieNode root, int x) { int queryMax = 0; TrieNode curr = root; for (int i = MAXD; i >= 0; i--) { if ((x & (1 << i)) != 0) { if (curr.children[0] != null && curr.children[0].count > 0) { queryMax |= 1 << i; curr = curr.children[0]; } else curr = curr.children[1]; } else { if (curr.children[1] != null && curr.children[1].count > 0) { queryMax |= 1 << i; curr = curr.children[1]; } else curr = curr.children[0]; } } return queryMax; } public void erase(TrieNode root, int x) { TrieNode curr = root; for (int i = MAXD; i >= 0; i--) { if ((x & (1 << i)) != 0) curr = curr.children[1]; else curr = curr.children[0]; curr.count--; } } public void depthFirstSearch(int[] ans, TrieNode root, int node, List<List<Integer>> edges, List<List<int[]>> stored) { insert(root, node); List<int[]> list = stored.get(node); for (int[] pair : list) { int index = pair[0], num = pair[1]; ans[index] = query(root, num); } List<Integer> nextNodes = edges.get(node); for (int nextNode : nextNodes) depthFirstSearch(ans, root, nextNode, edges, stored); erase(root, node); } } class TrieNode { int count; TrieNode[] children; public TrieNode() { children = new TrieNode[2]; count = 0; } } -
// OJ: https://leetcode.com/problems/maximum-genetic-difference-query/ // Time: O(P + Q) // Space: O(P) struct TrieNode { TrieNode *next[2] = {}; int cnt = 0; }; class Solution { public: vector<int> maxGeneticDifference(vector<int>& P, vector<vector<int>>& Q) { int N = P.size(), M = Q.size(), rootIndex; vector<vector<int>> G(N); for (int i = 0; i < N; ++i) { if (P[i] != -1) G[P[i]].push_back(i); else rootIndex = i; } unordered_map<int, vector<int>> m; for (int i = 0; i < M; ++i) m[Q[i][0]].push_back(i); TrieNode root; auto getAnswer = [&](TrieNode *node, int q) { int ans = 0; for (int i = 31; i >= 0; --i) { int b = q >> i & 1; if (node->next[1 - b] && node->next[1 - b]->cnt) { node = node->next[1 - b]; ans |= 1 << i; } else node = node->next[b]; } return ans; }; vector<int> ans(M); function<void(int)> dfs = [&](int u) { auto node = &root; for (int i = 31; i >= 0; --i) { int b = u >> i & 1; if (!node->next[b]) node->next[b] = new TrieNode(); node = node->next[b]; node->cnt++; } if (m.count(u)) { for (int index : m[u]) ans[index] = getAnswer(&root, Q[index][1]); } for (int v : G[u]) dfs(v); node = &root; for (int i = 31; i >= 0; --i) { int b = u >> i & 1; node = node->next[b]; node->cnt--; } }; dfs(rootIndex); return ans; } };