Welcome to Subscribe On Youtube
1928. Minimum Cost to Reach Destination in Time
Description
There is a country of n cities numbered from 0 to n - 1 where all the cities are connected by bi-directional roads. The roads are represented as a 2D integer array edges where edges[i] = [xi, yi, timei] denotes a road between cities xi and yi that takes timei minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a 0-indexed integer array passingFees of length n where passingFees[j] is the amount of dollars you must pay when you pass through city j.
In the beginning, you are at city 0 and want to reach city n - 1 in maxTime minutes or less. The cost of your journey is the summation of passing fees for each city that you passed through at some moment of your journey (including the source and destination cities).
Given maxTime, edges, and passingFees, return the minimum cost to complete your journey, or -1 if you cannot complete it within maxTime minutes.
Example 1:
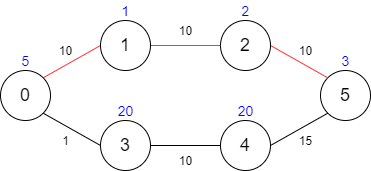
Input: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] Output: 11 Explanation: The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has 11 worth of passing fees.
Example 2:
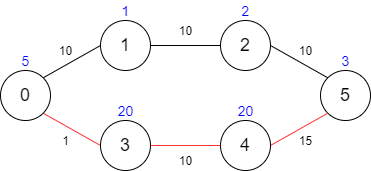
Input: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] Output: 48 Explanation: The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has 48 worth of passing fees. You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
Example 3:
Input: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3] Output: -1 Explanation: There is no way to reach city 5 from city 0 within 25 minutes.
Constraints:
1 <= maxTime <= 1000n == passingFees.length2 <= n <= 1000n - 1 <= edges.length <= 10000 <= xi, yi <= n - 11 <= timei <= 10001 <= passingFees[j] <= 1000- The graph may contain multiple edges between two nodes.
- The graph does not contain self loops.
Solution
First, use maps to store each city’s adjacent cities and corresponding times. Next, use dynamic programming to find the minimum cost. Create a 2D array costs where costs[i][j] is the minimum cost to reach i at time j, with 0 <= i < n and 0 <= j <= maxTime. Starting from city 0, find the minimum values of all elements in costs. Finally, return the minimum value in costs[n - 1], or -1 if it is impossible to reach city n - 1 within maxTime.
-
class Solution { public int minCost(int maxTime, int[][] edges, int[] passingFees) { int n = passingFees.length; int[][] times = new int[n][n]; for (int i = 0; i < n; i++) Arrays.fill(times[i], Integer.MAX_VALUE); for (int[] edge : edges) { int x = edge[0], y = edge[1], time = edge[2]; if (x > y) { int temp = x; x = y; y = temp; } if (time <= maxTime && time < times[x][y]) { times[x][y] = time; times[y][x] = time; } } Map<Integer, Integer>[] map = new Map[n]; for (int i = 0; i < n; i++) map[i] = new HashMap<Integer, Integer>(); for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if (times[i][j] != Integer.MAX_VALUE) { map[i].put(j, times[i][j]); map[j].put(i, times[i][j]); } } } int[][] costs = new int[n][maxTime + 1]; for (int i = 0; i < n; i++) Arrays.fill(costs[i], Integer.MAX_VALUE); costs[0][0] = passingFees[0]; PriorityQueue<int[]> priorityQueue = new PriorityQueue<int[]>(new Comparator<int[]>() { public int compare(int[] indexTimeCost1, int[] indexTimeCost2) { if (indexTimeCost1[2] != indexTimeCost2[2]) return indexTimeCost1[2] - indexTimeCost2[2]; else return indexTimeCost1[1] - indexTimeCost2[1]; } }); priorityQueue.offer(new int[]{0, 0, passingFees[0]}); while (!priorityQueue.isEmpty()) { int[] indexTimeCost = priorityQueue.poll(); int index = indexTimeCost[0], time = indexTimeCost[1], cost = indexTimeCost[2]; Map<Integer, Integer> nextMap = map[index]; for (Map.Entry<Integer, Integer> entry : nextMap.entrySet()) { int nextIndex = entry.getKey(), nextTime = entry.getValue(); int totalTime = time + nextTime; if (totalTime <= maxTime) { int totalCost = cost + passingFees[nextIndex]; if (totalCost < costs[nextIndex][totalTime]) { costs[nextIndex][totalTime] = totalCost; priorityQueue.offer(new int[]{nextIndex, totalTime, totalCost}); } } } } int minCost = Integer.MAX_VALUE; for (int i = 0; i <= maxTime; i++) minCost = Math.min(minCost, costs[n - 1][i]); return minCost == Integer.MAX_VALUE ? -1 : minCost; } } -
// OJ: https://leetcode.com/problems/minimum-cost-to-reach-destination-in-time/ // Time: O(ElogE) // Space: O(V + E) class Solution { typedef array<int, 3> Node; // node, time, cost public: int minCost(int maxTime, vector<vector<int>>& E, vector<int>& F) { int N = F.size(); vector<unordered_map<int, int>> G(N); vector<int> minTime(N, maxTime + 1); for (auto &e : E) { int u = e[0], v = e[1], t = e[2]; if (G[u].count(v)) { // For duplicated edges, we just need to keep track of the edge with smallest time. G[u][v] = G[v][u] = min(G[u][v], t); } else { G[u][v] = G[v][u] = t; } } auto cmp = [](auto &a, auto &b) { return a[2] > b[2]; }; // min-heap: Heap top is the node with the smallest cost to reach priority_queue<Node, vector<Node>, decltype(cmp)> pq(cmp); pq.push({0, 0, F[0]}); minTime[0] = 0; while (pq.size()) { auto [u, time, c] = pq.top(); pq.pop(); if (u == N - 1) return c; for (auto &[v, t] : G[u]) { int nt = time + t, nc = c + F[v]; if (nt < minTime[v]) { minTime[v] = nt; pq.push({v, nt, nc}); } } } return -1; } }; -
class Solution: def minCost( self, maxTime: int, edges: List[List[int]], passingFees: List[int] ) -> int: m, n = maxTime, len(passingFees) f = [[inf] * n for _ in range(m + 1)] f[0][0] = passingFees[0] for i in range(1, m + 1): for x, y, t in edges: if t <= i: f[i][x] = min(f[i][x], f[i - t][y] + passingFees[x]) f[i][y] = min(f[i][y], f[i - t][x] + passingFees[y]) ans = min(f[i][n - 1] for i in range(m + 1)) return ans if ans < inf else -1 -
func minCost(maxTime int, edges [][]int, passingFees []int) int { m, n := maxTime, len(passingFees) f := make([][]int, m+1) const inf int = 1 << 30 for i := range f { f[i] = make([]int, n) for j := range f[i] { f[i][j] = inf } } f[0][0] = passingFees[0] for i := 1; i <= m; i++ { for _, e := range edges { x, y, t := e[0], e[1], e[2] if t <= i { f[i][x] = min(f[i][x], f[i-t][y]+passingFees[x]) f[i][y] = min(f[i][y], f[i-t][x]+passingFees[y]) } } } ans := inf for i := 1; i <= m; i++ { ans = min(ans, f[i][n-1]) } if ans == inf { return -1 } return ans } -
function minCost(maxTime: number, edges: number[][], passingFees: number[]): number { const [m, n] = [maxTime, passingFees.length]; const f: number[][] = Array.from({ length: m + 1 }, () => Array(n).fill(Infinity)); f[0][0] = passingFees[0]; for (let i = 1; i <= m; ++i) { for (const [x, y, t] of edges) { if (t <= i) { f[i][x] = Math.min(f[i][x], f[i - t][y] + passingFees[x]); f[i][y] = Math.min(f[i][y], f[i - t][x] + passingFees[y]); } } } let ans = Infinity; for (let i = 1; i <= m; ++i) { ans = Math.min(ans, f[i][n - 1]); } return ans === Infinity ? -1 : ans; }