Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1727.html
1727. Largest Submatrix With Rearrangements
Level
Medium
Description
You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.
Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.
Example 1:
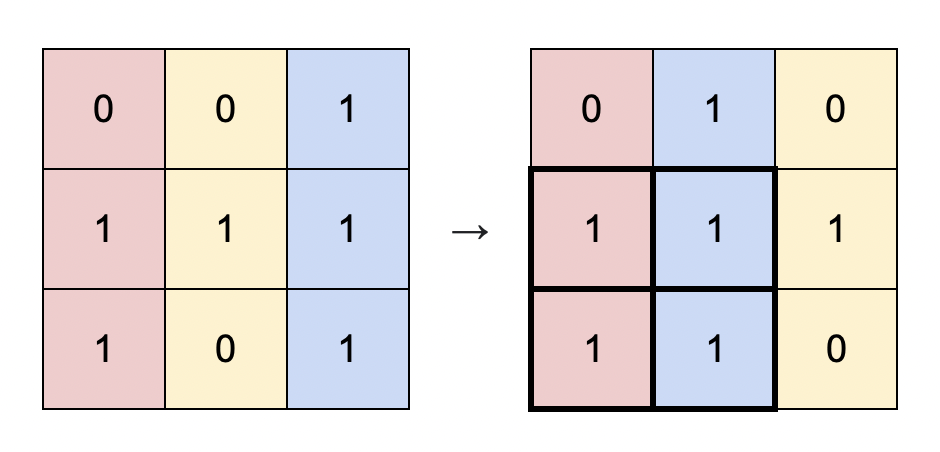
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.
Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.
Example 3:
Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.
Example 4:
Input: matrix = [[0,0],[0,0]]
Output: 0
Explanation: As there are no 1s, no submatrix of 1s can be formed and the area is 0.
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m * n <= 10^5matrix[i][j]is0or1.
Solution
For each element in matrix, calculate the number of consecutive 1’s above the element. Concretely, if matrix[i][j] == 1, then find the minimum k such that for all k <= p <= i, there is matrix[p][j] == 1. Create newMatrix with the same size as matrix, and set newMatrix[i][j] = i - k + 1 where k is defined above.
Then for each row curRow in newMatrix, sort curRow and loop over curRow backwards. For curRow[j], the current area is calculated as (n - j) * curRow[j]. Maintain the maximum area in the process.
Finally, return the maximum area.
-
class Solution { public int largestSubmatrix(int[][] matrix) { int maxArea = 0; int rows = matrix.length, columns = matrix[0].length; int[][] newMatrix = new int[rows][columns]; for (int j = 0; j < columns; j++) newMatrix[0][j] = matrix[0][j]; for (int i = 1; i < rows; i++) { for (int j = 0; j < columns; j++) { if (matrix[i][j] == 1) newMatrix[i][j] = newMatrix[i - 1][j] + 1; } } for (int i = 0; i < rows; i++) { int[] curRow = new int[columns]; System.arraycopy(newMatrix[i], 0, curRow, 0, columns); Arrays.sort(curRow); for (int j = columns - 1; j >= 0; j--) { if (curRow[j] == 0) break; int area = (columns - j) * curRow[j]; maxArea = Math.max(maxArea, area); } } return maxArea; } } ############ class Solution { public int largestSubmatrix(int[][] matrix) { int m = matrix.length, n = matrix[0].length; for (int i = 1; i < m; ++i) { for (int j = 0; j < n; ++j) { if (matrix[i][j] == 1) { matrix[i][j] = matrix[i - 1][j] + 1; } } } int ans = 0; for (var row : matrix) { Arrays.sort(row); for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) { int s = row[j] * k; ans = Math.max(ans, s); } } return ans; } } -
// OJ: https://leetcode.com/problems/largest-submatrix-with-rearrangements/ // Time: O(MNlogN) // Space: O(N) class Solution { public: int largestSubmatrix(vector<vector<int>>& A) { int M = A.size(), N = A[0].size(), ans = 0; vector<int> h(N); for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { h[j] = A[i][j] == 0 ? 0 : (h[j] + 1); } map<int, int> m; for (int n : h) m[n]++; int w = 0; for (auto it = m.rbegin(); it != m.rend(); ++it) { w += it->second; ans = max(ans, w * it->first); } } return ans; } }; -
class Solution: def largestSubmatrix(self, matrix: List[List[int]]) -> int: for i in range(1, len(matrix)): for j in range(len(matrix[0])): if matrix[i][j]: matrix[i][j] = matrix[i - 1][j] + 1 ans = 0 for row in matrix: row.sort(reverse=True) for j, v in enumerate(row, 1): ans = max(ans, j * v) return ans ############ # 1727. Largest Submatrix With Rearrangements # https://leetcode.com/problems/largest-submatrix-with-rearrangements/ class Solution: def largestSubmatrix(self, A: List[List[int]]): rows, cols = len(A), len(A[0]) for i in range(1,rows): for j in range(cols): if A[i][j] == 1: A[i][j] += A[i-1][j] res = 0 for i in range(rows): row = sorted(A[i]) for j in range(cols): res = max(res, row[j] * (cols - j)) return res -
func largestSubmatrix(matrix [][]int) int { m, n := len(matrix), len(matrix[0]) for i := 1; i < m; i++ { for j := 0; j < n; j++ { if matrix[i][j] == 1 { matrix[i][j] = matrix[i-1][j] + 1 } } } ans := 0 for _, row := range matrix { sort.Ints(row) for j, k := n-1, 1; j >= 0 && row[j] > 0; j, k = j-1, k+1 { ans = max(ans, row[j]*k) } } return ans } func max(a, b int) int { if a > b { return a } return b } -
function largestSubmatrix(matrix: number[][]): number { for (let column = 0; column < matrix[0].length; column++) { for (let row = 0; row < matrix.length; row++) { let tempRow = row; let count = 0; while (tempRow < matrix.length && matrix[tempRow][column] === 1) { count++; tempRow++; } while (count !== 0) { matrix[row][column] = count; count--; row++; } } } for (let row = 0; row < matrix.length; row++) { matrix[row].sort((a, b) => a - b); } let maxSubmatrixArea = 0; for (let row = 0; row < matrix.length; row++) { for (let col = matrix[row].length - 1; col >= 0; col--) { maxSubmatrixArea = Math.max( maxSubmatrixArea, matrix[row][col] * (matrix[row].length - col), ); } } return maxSubmatrixArea; }