Formatted question description: https://leetcode.ca/all/1724.html

1724. Checking Existence of Edge Length Limited Paths II

Level

Hard

Description

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [u_i, v_i, dis_i] denotes an edge between nodes u_i and v_i with distance dis_i. Note that there may be multiple edges between two nodes, and the graph may not be connected.

Implement the DistanceLimitedPathsExist class:

DistanceLimitedPathsExist(int n, int[][] edgeList) Initializes the class with an undirected graph.
boolean query(int p, int q, int limit) Returns true if there exists a path from p to q such that each edge on the path has a distance strictly less than limit, and otherwise false.

Example 1:

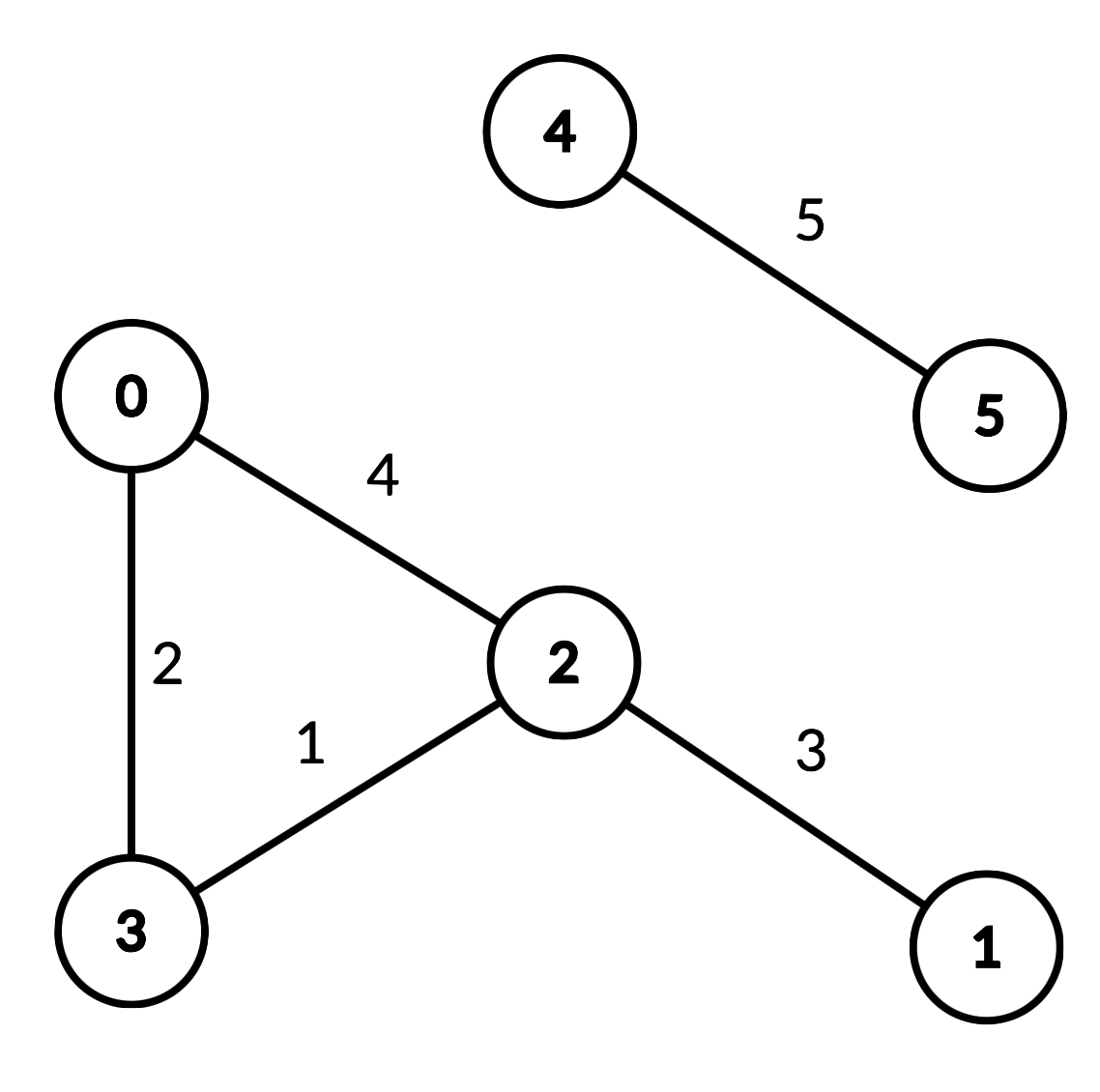
Image text

Input
["DistanceLimitedPathsExist", "query", "query", "query", "query"]
[[6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]], [2, 3, 2], [1, 3, 3], [2, 0, 3], [0, 5, 6]]
Output
[null, true, false, true, false]

Explanation
DistanceLimitedPathsExist distanceLimitedPathsExist = new DistanceLimitedPathsExist(6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]);
distanceLimitedPathsExist.query(2, 3, 2); // return true. There is an edge from 2 to 3 of distance 1, which is less than 2.
distanceLimitedPathsExist.query(1, 3, 3); // return false. There is no way to go from 1 to 3 with distances strictly less than 3.
distanceLimitedPathsExist.query(2, 0, 3); // return true. There is a way to go from 2 to 0 with distance < 3: travel from 2 to 3 to 0.
distanceLimitedPathsExist.query(0, 5, 6); // return false. There are no paths from 0 to 5.

Constraints:

2 <= n <= 10^4
0 <= edgeList.length <= 10^4
edgeList[i].length == 3
0 <= u_i, v_i, p, q <= n-1
u_i != v_i
p != q
1 <= dis_i, limit <= 10^9
At most 10^4 calls will be made to query.

Solution

The main idea of this problem is to create a minimum spanning tree from the edges and the nodes. In the constructor, create a minimum spanning tree using union find and Kruskal’s algorithm. For the method query, the idea is similar to finding the lowest common ancestor.

class DistanceLimitedPathsExist {
    int n;
    int bits;
    UnionFind uf;
    int[][] edgeList;
    Map<Integer, List<int[]>> mstEdges;
    int[][] parent;
    int[][] maxWeights;
    int[] depths;
    boolean[] visited;

    public DistanceLimitedPathsExist(int n, int[][] edgeList) {
        this.n = n;
        this.uf = new UnionFind(n);
        this.edgeList = edgeList;
        Arrays.sort(this.edgeList, new Comparator<int[]>() {
            public int compare(int[] edge1, int[] edge2) {
                return edge1[2] - edge2[2];
            }
        });
        mstEdges = new HashMap<Integer, List<int[]>>();
        bits = (int) (Math.log(n) / Math.log(2)) + 2;
        this.parent = new int[n][bits];
        for (int i = 0; i < n; i++)
            Arrays.fill(this.parent[i], -1);
        this.maxWeights = new int[n][bits];
        this.depths = new int[n];
        this.visited = new boolean[n];
        kruskal();
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                depths[i] = 1;
                depthFirstSearch(i);
                parent[i][0] = i;
            }
        }
        for (int i = 1; i < bits; i++) {
            for (int j = 0; j < n; j++) {
                parent[j][i] = parent[parent[j][i - 1]][i - 1];
                maxWeights[j][i] = Math.max(maxWeights[j][i - 1], maxWeights[parent[j][i - 1]][i - 1]);
            }
        }
    }
    
    public boolean query(int p, int q, int limit) {
        if (uf.find(p) != uf.find(q))
            return false;
        else
            return lowestCommonAncestor(p, q) < limit;
    }

    private void kruskal() {
        int edgesCount = edgeList.length;
        for (int i = 0; i < edgesCount; i++) {
            int[] edge = edgeList[i];
            int u = edge[0], v = edge[1], dist = edge[2];
            if (uf.union(u, v)) {
                List<int[]> list1 = mstEdges.getOrDefault(u, new ArrayList<int[]>());
                List<int[]> list2 = mstEdges.getOrDefault(v, new ArrayList<int[]>());
                list1.add(new int[]{v, dist});
                list2.add(new int[]{u, dist});
                mstEdges.put(u, list1);
                mstEdges.put(v, list2);
            }
        }
    }

    private void depthFirstSearch(int u) {
        visited[u] = true;
        List<int[]> list = mstEdges.getOrDefault(u, new ArrayList<int[]>());
        for (int[] array : list) {
            int v = array[0], dist = array[1];
            if (!visited[v]) {
                depths[v] = depths[u] + 1;
                parent[v][0] = u;
                maxWeights[v][0] = dist;
                depthFirstSearch(v);
            }
        }
    }

    private int lowestCommonAncestor(int u, int v) {
        if (depths[u] > depths[v]) {
            int temp = u;
            u = v;
            v = temp;
        }
        int temp = depths[v] - depths[u];
        int weight = 0;
        int index = 0;
        while (temp != 0) {
            if (temp % 2 != 0) {
                weight = Math.max(weight, maxWeights[v][index]);
                v = parent[v][index];
            }
            temp >>= 1;
            index++;
        }
        if (u == v)
            return weight;
        for (int i = bits - 1; i >= 0; i--) {
            if (parent[u][i] != parent[v][i]) {
                weight = Math.max(weight, Math.max(maxWeights[u][i], maxWeights[v][i]));
                u = parent[u][i];
                v = parent[v][i];
            }
        }
        weight = Math.max(weight, Math.max(maxWeights[u][0], maxWeights[v][0]));
        return weight;
    }
}

class UnionFind {
    int n;
    int[] parent;

    public UnionFind(int n) {
        this.n = n;
        this.parent = new int[n];
        for (int i = 0; i < n; i++) {
            this.parent[i] = i;
        }
    }

    public boolean union(int index1, int index2) {
        int ancestor1 = find(index1), ancestor2 = find(index2);
        if (ancestor1 == ancestor2)
            return false;
        else {
            parent[find(index2)] = find(index1);
            return true;
        }
    }

    public int find(int index) {
        if (parent[index] != index)
            parent[index] = find(parent[index]);
        return parent[index];
    }
}

/**
 * Your DistanceLimitedPathsExist object will be instantiated and called as such:
 * DistanceLimitedPathsExist obj = new DistanceLimitedPathsExist(n, edgeList);
 * boolean param_1 = obj.query(p,q,limit);
 */

class PersistentUnionFind {
private:
    vector<int> rank;
    vector<int> parent;
    vector<int> version;

public:
    PersistentUnionFind(int n)
        : rank(n, 0)
        , parent(n)
        , version(n, INT_MAX) {
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    int find(int x, int t) {
        if (parent[x] == x || version[x] >= t) {
            return x;
        }
        return find(parent[x], t);
    }

    bool unionSet(int a, int b, int t) {
        int pa = find(a, INT_MAX);
        int pb = find(b, INT_MAX);
        if (pa == pb) {
            return false;
        }
        if (rank[pa] > rank[pb]) {
            version[pb] = t;
            parent[pb] = pa;
        } else {
            version[pa] = t;
            parent[pa] = pb;
            if (rank[pa] == rank[pb]) {
                rank[pb]++;
            }
        }
        return true;
    }
};

class DistanceLimitedPathsExist {
private:
    PersistentUnionFind puf;

public:
    DistanceLimitedPathsExist(int n, vector<vector<int>>& edgeList)
        : puf(n) {
        sort(edgeList.begin(), edgeList.end(),
            [](const vector<int>& a, const vector<int>& b) {
                return a[2] < b[2];
            });

        for (const auto& edge : edgeList) {
            puf.unionSet(edge[0], edge[1], edge[2]);
        }
    }

    bool query(int p, int q, int limit) {
        return puf.find(p, limit) == puf.find(q, limit);
    }
};

/**
 * Your DistanceLimitedPathsExist object will be instantiated and called as such:
 * DistanceLimitedPathsExist* obj = new DistanceLimitedPathsExist(n, edgeList);
 * bool param_1 = obj->query(p,q,limit);
 */

class PersistentUnionFind:
    def __init__(self, n):
        self.rank = [0] * n
        self.p = list(range(n))
        self.version = [inf] * n

    def find(self, x, t=inf):
        if self.p[x] == x or self.version[x] >= t:
            return x
        return self.find(self.p[x], t)

    def union(self, a, b, t):
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.rank[pa] > self.rank[pb]:
            self.version[pb] = t
            self.p[pb] = pa
        else:
            self.version[pa] = t
            self.p[pa] = pb
            if self.rank[pa] == self.rank[pb]:
                self.rank[pb] += 1
        return True


class DistanceLimitedPathsExist:
    def __init__(self, n: int, edgeList: List[List[int]]):
        self.puf = PersistentUnionFind(n)
        edgeList.sort(key=lambda x: x[2])
        for u, v, dis in edgeList:
            self.puf.union(u, v, dis)

    def query(self, p: int, q: int, limit: int) -> bool:
        return self.puf.find(p, limit) == self.puf.find(q, limit)

type PersistentUnionFind struct {
	rank    []int
	parent  []int
	version []int
}

func NewPersistentUnionFind(n int) *PersistentUnionFind {
	rank := make([]int, n)
	parent := make([]int, n)
	version := make([]int, n)

	for i := 0; i < n; i++ {
		parent[i] = i
	}

	return &PersistentUnionFind{
		rank:    rank,
		parent:  parent,
		version: version,
	}
}

func (uf *PersistentUnionFind) find(x int, t int) int {
	if uf.parent[x] == x || uf.version[x] >= t {
		return x
	}
	return uf.find(uf.parent[x], t)
}

func (uf *PersistentUnionFind) union(a, b, t int) bool {
	pa := uf.find(a, int(^uint(0)>>1))
	pb := uf.find(b, int(^uint(0)>>1))

	if pa == pb {
		return false
	}

	if uf.rank[pa] > uf.rank[pb] {
		uf.version[pb] = t
		uf.parent[pb] = pa
	} else {
		uf.version[pa] = t
		uf.parent[pa] = pb
		if uf.rank[pa] == uf.rank[pb] {
			uf.rank[pb]++
		}
	}

	return true
}

type DistanceLimitedPathsExist struct {
	puf *PersistentUnionFind
}

func Constructor(n int, edgeList [][]int) DistanceLimitedPathsExist {
	sort.Slice(edgeList, func(i, j int) bool {
		return edgeList[i][2] < edgeList[j][2]
	})

	puf := NewPersistentUnionFind(n)

	for _, edge := range edgeList {
		puf.union(edge[0], edge[1], edge[2])
	}

	return DistanceLimitedPathsExist{
		puf: puf,
	}
}

func (dle *DistanceLimitedPathsExist) Query(p, q, limit int) bool {
	return dle.puf.find(p, limit) == dle.puf.find(q, limit)
}

/**
 * Your DistanceLimitedPathsExist object will be instantiated and called as such:
 * obj := Constructor(n, edgeList);
 * param_1 := obj.Query(p,q,limit);
 */

class PersistentUnionFind {
    private rank: number[];
    private parent: number[];
    private version: number[];

    constructor(n: number) {
        this.rank = Array(n).fill(0);
        this.parent = Array.from({ length: n }, (_, i) => i);
        this.version = Array(n).fill(Infinity);
    }

    find(x: number, t: number): number {
        if (this.parent[x] === x || this.version[x] >= t) {
            return x;
        }
        return this.find(this.parent[x], t);
    }

    union(a: number, b: number, t: number): boolean {
        const pa = this.find(a, Infinity);
        const pb = this.find(b, Infinity);

        if (pa === pb) {
            return false;
        }

        if (this.rank[pa] > this.rank[pb]) {
            this.version[pb] = t;
            this.parent[pb] = pa;
        } else {
            this.version[pa] = t;
            this.parent[pa] = pb;
            if (this.rank[pa] === this.rank[pb]) {
                this.rank[pb]++;
            }
        }

        return true;
    }
}

class DistanceLimitedPathsExist {
    private puf: PersistentUnionFind;

    constructor(n: number, edgeList: number[][]) {
        this.puf = new PersistentUnionFind(n);
        edgeList.sort((a, b) => a[2] - b[2]);
        for (const [u, v, dis] of edgeList) {
            this.puf.union(u, v, dis);
        }
    }

    query(p: number, q: number, limit: number): boolean {
        return this.puf.find(p, limit) === this.puf.find(q, limit);
    }
}

/**
 * Your DistanceLimitedPathsExist object will be instantiated and called as such:
 * var obj = new DistanceLimitedPathsExist(n, edgeList)
 * var param_1 = obj.query(p,q,limit)
 */

1724 - Checking Existence of Edge Length Limited Paths II

1724. Checking Existence of Edge Length Limited Paths II

Level

Description

Solution

All Problems

All Solutions

Welcome to Subscribe On Youtube

1724. Checking Existence of Edge Length Limited Paths II

Level

Description

Solution

All Problems

All Solutions