1914. Cyclically Rotating a Grid

Description

You are given an m x n integer matrix grid, where m and n are both even integers, and an integer k.

The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:

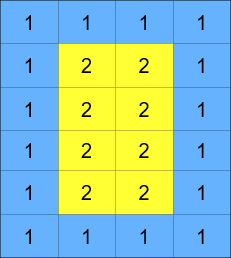
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:

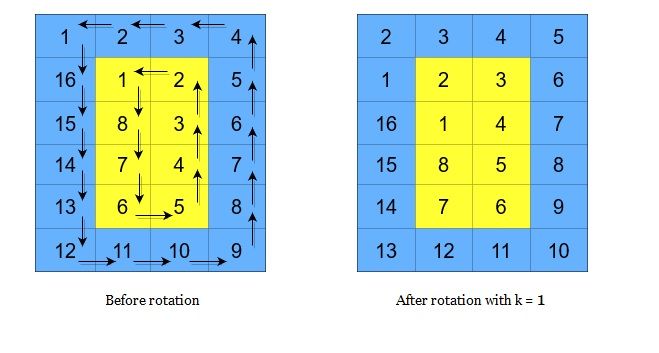
Return the matrix after applying k cyclic rotations to it.

Example 1:

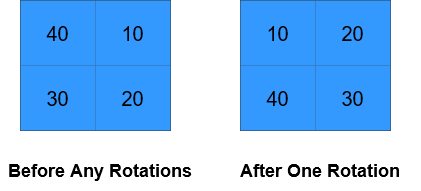
Input: grid = [[40,10],[30,20]], k = 1
Output: [[10,20],[40,30]]
Explanation: The figures above represent the grid at every state.

Example 2:

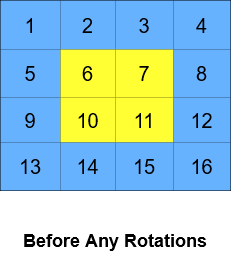
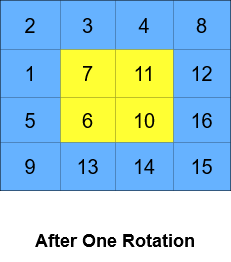
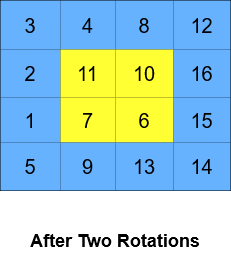
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
Explanation: The figures above represent the grid at every state.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 50
Both m and n are even integers.
1 <= grid[i][j] <=5000
1 <= k <= 10⁹

Solutions

class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int[][] rotateGrid(int[][] grid, int k) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        for (int p = 0; p < Math.min(m, n) / 2; ++p) {
            rotate(p, k);
        }
        return grid;
    }

    private void rotate(int p, int k) {
        List<Integer> nums = new ArrayList<>();
        for (int j = p; j < n - p - 1; ++j) {
            nums.add(grid[p][j]);
        }
        for (int i = p; i < m - p - 1; ++i) {
            nums.add(grid[i][n - p - 1]);
        }
        for (int j = n - p - 1; j > p; --j) {
            nums.add(grid[m - p - 1][j]);
        }
        for (int i = m - p - 1; i > p; --i) {
            nums.add(grid[i][p]);
        }
        int l = nums.size();
        k %= l;
        if (k == 0) {
            return;
        }
        for (int j = p; j < n - p - 1; ++j) {
            grid[p][j] = nums.get(k++ % l);
        }
        for (int i = p; i < m - p - 1; ++i) {
            grid[i][n - p - 1] = nums.get(k++ % l);
        }
        for (int j = n - p - 1; j > p; --j) {
            grid[m - p - 1][j] = nums.get(k++ % l);
        }
        for (int i = m - p - 1; i > p; --i) {
            grid[i][p] = nums.get(k++ % l);
        }
    }
}

class Solution {
public:
    vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
        int m = grid.size(), n = grid[0].size();
        auto rotate = [&](int p, int k) {
            vector<int> nums;
            for (int j = p; j < n - p - 1; ++j) {
                nums.push_back(grid[p][j]);
            }
            for (int i = p; i < m - p - 1; ++i) {
                nums.push_back(grid[i][n - p - 1]);
            }
            for (int j = n - p - 1; j > p; --j) {
                nums.push_back(grid[m - p - 1][j]);
            }
            for (int i = m - p - 1; i > p; --i) {
                nums.push_back(grid[i][p]);
            }
            int l = nums.size();
            k %= l;
            if (k == 0) {
                return;
            }
            for (int j = p; j < n - p - 1; ++j) {
                grid[p][j] = nums[k++ % l];
            }
            for (int i = p; i < m - p - 1; ++i) {
                grid[i][n - p - 1] = nums[k++ % l];
            }
            for (int j = n - p - 1; j > p; --j) {
                grid[m - p - 1][j] = nums[k++ % l];
            }
            for (int i = m - p - 1; i > p; --i) {
                grid[i][p] = nums[k++ % l];
            }
        };
        for (int p = 0; p < min(m, n) / 2; ++p) {
            rotate(p, k);
        }
        return grid;
    }
};

class Solution:
    def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        def rotate(p: int, k: int):
            nums = []
            for j in range(p, n - p - 1):
                nums.append(grid[p][j])
            for i in range(p, m - p - 1):
                nums.append(grid[i][n - p - 1])
            for j in range(n - p - 1, p, -1):
                nums.append(grid[m - p - 1][j])
            for i in range(m - p - 1, p, -1):
                nums.append(grid[i][p])
            k %= len(nums)
            if k == 0:
                return
            nums = nums[k:] + nums[:k]
            k = 0
            for j in range(p, n - p - 1):
                grid[p][j] = nums[k]
                k += 1
            for i in range(p, m - p - 1):
                grid[i][n - p - 1] = nums[k]
                k += 1
            for j in range(n - p - 1, p, -1):
                grid[m - p - 1][j] = nums[k]
                k += 1
            for i in range(m - p - 1, p, -1):
                grid[i][p] = nums[k]
                k += 1

        m, n = len(grid), len(grid[0])
        for p in range(min(m, n) >> 1):
            rotate(p, k)
        return grid

func rotateGrid(grid [][]int, k int) [][]int {
	m, n := len(grid), len(grid[0])

	rotate := func(p, k int) {
		nums := []int{}
		for j := p; j < n-p-1; j++ {
			nums = append(nums, grid[p][j])
		}
		for i := p; i < m-p-1; i++ {
			nums = append(nums, grid[i][n-p-1])
		}
		for j := n - p - 1; j > p; j-- {
			nums = append(nums, grid[m-p-1][j])
		}
		for i := m - p - 1; i > p; i-- {
			nums = append(nums, grid[i][p])
		}
		l := len(nums)
		k %= l
		if k == 0 {
			return
		}
		for j := p; j < n-p-1; j++ {
			grid[p][j] = nums[k]
			k = (k + 1) % l
		}
		for i := p; i < m-p-1; i++ {
			grid[i][n-p-1] = nums[k]
			k = (k + 1) % l
		}
		for j := n - p - 1; j > p; j-- {
			grid[m-p-1][j] = nums[k]
			k = (k + 1) % l
		}
		for i := m - p - 1; i > p; i-- {
			grid[i][p] = nums[k]
			k = (k + 1) % l
		}
	}

	for i := 0; i < m/2 && i < n/2; i++ {
		rotate(i, k)
	}
	return grid
}

function rotateGrid(grid: number[][], k: number): number[][] {
    const m = grid.length;
    const n = grid[0].length;
    const rotate = (p: number, k: number) => {
        const nums: number[] = [];
        for (let j = p; j < n - p - 1; ++j) {
            nums.push(grid[p][j]);
        }
        for (let i = p; i < m - p - 1; ++i) {
            nums.push(grid[i][n - p - 1]);
        }
        for (let j = n - p - 1; j > p; --j) {
            nums.push(grid[m - p - 1][j]);
        }
        for (let i = m - p - 1; i > p; --i) {
            nums.push(grid[i][p]);
        }
        const l = nums.length;
        k %= l;
        if (k === 0) {
            return;
        }
        for (let j = p; j < n - p - 1; ++j) {
            grid[p][j] = nums[k++ % l];
        }
        for (let i = p; i < m - p - 1; ++i) {
            grid[i][n - p - 1] = nums[k++ % l];
        }
        for (let j = n - p - 1; j > p; --j) {
            grid[m - p - 1][j] = nums[k++ % l];
        }
        for (let i = m - p - 1; i > p; --i) {
            grid[i][p] = nums[k++ % l];
        }
    };
    for (let p = 0; p < Math.min(m, n) >> 1; ++p) {
        rotate(p, k);
    }
    return grid;
}

1914 - Cyclically Rotating a Grid

1914. Cyclically Rotating a Grid

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1914. Cyclically Rotating a Grid

Description

Solutions

All Problems

All Solutions