Welcome to Subscribe On Youtube

1886. Determine Whether Matrix Can Be Obtained By Rotation

Description

Given two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.

 

Example 1:

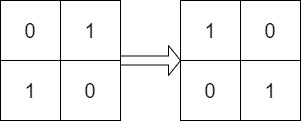
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.

Example 2:

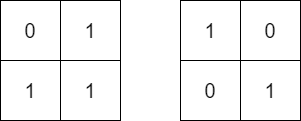
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
Output: false
Explanation: It is impossible to make mat equal to target by rotating mat.

Example 3:

Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.

 

Constraints:

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] and target[i][j] are either 0 or 1.

Solutions

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public boolean findRotation(int[][] mat, int[][] target) {
          int times = 4;
          while (times-- > 0) {
              if (equals(mat, target)) {
                  return true;
              }
              rotate(mat);
          }
          return false;
      }
  
      private void rotate(int[][] matrix) {
          int n = matrix.length;
          for (int i = 0; i < n / 2; ++i) {
              for (int j = i; j < n - 1 - i; ++j) {
                  int t = matrix[i][j];
                  matrix[i][j] = matrix[n - j - 1][i];
                  matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                  matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                  matrix[j][n - i - 1] = t;
              }
          }
      }
  
      private boolean equals(int[][] nums1, int[][] nums2) {
          int n = nums1.length;
          for (int i = 0; i < n; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (nums1[i][j] != nums2[i][j]) {
                      return false;
                  }
              }
          }
          return true;
      }
  }
  

• class Solution {
  public:
      bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
          int n = mat.size();
          for (int k = 0; k < 4; ++k) {
              vector<vector<int>> g(n, vector<int>(n));
              for (int i = 0; i < n; ++i)
                  for (int j = 0; j < n; ++j)
                      g[i][j] = mat[j][n - i - 1];
              if (g == target) return true;
              mat = g;
          }
          return false;
      }
  };
  

• class Solution:
      def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
          def rotate(matrix):
              n = len(matrix)
              for i in range(n // 2):
                  for j in range(i, n - 1 - i):
                      t = matrix[i][j]
                      matrix[i][j] = matrix[n - j - 1][i]
                      matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
                      matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
                      matrix[j][n - i - 1] = t
  
          for _ in range(4):
              if mat == target:
                  return True
              rotate(mat)
          return False
  
  

• func findRotation(mat [][]int, target [][]int) bool {
  	n := len(mat)
  	for k := 0; k < 4; k++ {
  		g := make([][]int, n)
  		for i := range g {
  			g[i] = make([]int, n)
  		}
  		for i := 0; i < n; i++ {
  			for j := 0; j < n; j++ {
  				g[i][j] = mat[j][n-i-1]
  			}
  		}
  		if equals(g, target) {
  			return true
  		}
  		mat = g
  	}
  	return false
  }
  
  func equals(a, b [][]int) bool {
  	for i, row := range a {
  		for j, v := range row {
  			if v != b[i][j] {
  				return false
  			}
  		}
  	}
  	return true
  }
  

• function findRotation(mat: number[][], target: number[][]): boolean {
      for (let k = 0; k < 4; k++) {
          rotate(mat);
          if (isEqual(mat, target)) {
              return true;
          }
      }
      return false;
  }
  
  function isEqual(A: number[][], B: number[][]) {
      const n = A.length;
      for (let i = 0; i < n; i++) {
          for (let j = 0; j < n; j++) {
              if (A[i][j] !== B[i][j]) {
                  return false;
              }
          }
      }
      return true;
  }
  
  function rotate(matrix: number[][]): void {
      const n = matrix.length;
      for (let i = 0; i < n >> 1; i++) {
          for (let j = 0; j < (n + 1) >> 1; j++) {
              [
                  matrix[i][j],
                  matrix[n - 1 - j][i],
                  matrix[n - 1 - i][n - 1 - j],
                  matrix[j][n - 1 - i],
              ] = [
                  matrix[n - 1 - j][i],
                  matrix[n - 1 - i][n - 1 - j],
                  matrix[j][n - 1 - i],
                  matrix[i][j],
              ];
          }
      }
  }
  
  

• impl Solution {
      pub fn find_rotation(mat: Vec<Vec<i32>>, target: Vec<Vec<i32>>) -> bool {
          let n = mat.len();
          let mut is_equal = [true; 4];
          for i in 0..n {
              for j in 0..n {
                  if is_equal[0] && mat[i][j] != target[i][j] {
                      is_equal[0] = false;
                  }
                  if is_equal[1] && mat[i][j] != target[j][n - 1 - i] {
                      is_equal[1] = false;
                  }
                  if is_equal[2] && mat[i][j] != target[n - 1 - i][n - 1 - j] {
                      is_equal[2] = false;
                  }
                  if is_equal[3] && mat[i][j] != target[n - 1 - j][i] {
                      is_equal[3] = false;
                  }
              }
          }
          is_equal.into_iter().any(|&v| v)
      }
  }
  
  

All Problems

All Solutions