Welcome to Subscribe On Youtube
1878. Get Biggest Three Rhombus Sums in a Grid
Description
You are given an m x n integer matrix grid.
A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:
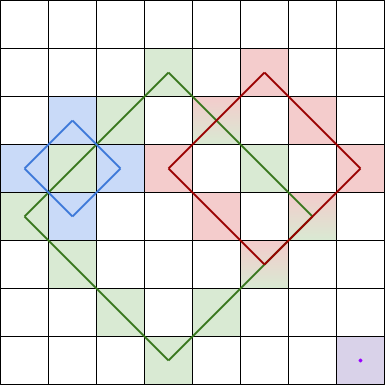
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.
Return the biggest three distinct rhombus sums in the grid in descending order. If there are less than three distinct values, return all of them.
Example 1:
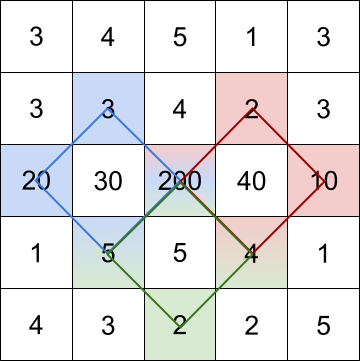
Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]] Output: [228,216,211] Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above. - Blue: 20 + 3 + 200 + 5 = 228 - Red: 200 + 2 + 10 + 4 = 216 - Green: 5 + 200 + 4 + 2 = 211
Example 2:
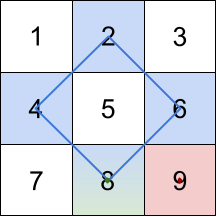
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: [20,9,8] Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above. - Blue: 4 + 2 + 6 + 8 = 20 - Red: 9 (area 0 rhombus in the bottom right corner) - Green: 8 (area 0 rhombus in the bottom middle)
Example 3:
Input: grid = [[7,7,7]] Output: [7] Explanation: All three possible rhombus sums are the same, so return [7].
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 105
Solutions
Solution 1: Enumerate Diamond Center + Prefix Sum + Ordered Set
We can preprocess to get two prefix sum arrays $s_1$ and $s_2$, where $s_1[i][j]$ represents the sum of the elements on the upper left diagonal ending at $(i, j)$, and $s_2[i][j]$ represents the sum of the elements on the upper right diagonal ending at $(i, j)$.
Next, we enumerate each position $(i, j)$, first add $grid[i][j]$ to the ordered set $ss$, and then enumerate the length $k$ of the diamond. The sum of the diamond with $(i, j)$ as the center and a side length of $k$ is:
\[\begin{aligned} &\quad s_1[i + k][j] - s_1[i][j - k] + s_1[i][j + k] - s_1[i - k][j] \\ &+ s_2[i][j - k] - s_2[i - k][j] + s_2[i + k][j] - s_2[i][j + k] \\ &- grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1] \end{aligned}\]We add this value to the ordered set $ss$, while ensuring that the size of the ordered set $ss$ does not exceed $3$. Finally, we output the elements in the ordered set $ss$ in reverse order.
The time complexity is $O(m \times n \times \min(m, n))$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.
-
class Solution { public int[] getBiggestThree(int[][] grid) { int m = grid.length, n = grid[0].length; int[][] s1 = new int[m + 1][n + 2]; int[][] s2 = new int[m + 1][n + 2]; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1]; s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1]; } } TreeSet<Integer> ss = new TreeSet<>(); for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { int l = Math.min(Math.min(i - 1, m - i), Math.min(j - 1, n - j)); ss.add(grid[i - 1][j - 1]); for (int k = 1; k <= l; ++k) { int a = s1[i + k][j] - s1[i][j - k]; int b = s1[i][j + k] - s1[i - k][j]; int c = s2[i][j - k] - s2[i - k][j]; int d = s2[i + k][j] - s2[i][j + k]; ss.add(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]); } while (ss.size() > 3) { ss.pollFirst(); } } } int[] ans = new int[ss.size()]; for (int i = 0; i < ans.length; ++i) { ans[i] = ss.pollLast(); } return ans; } } -
class Solution { public: vector<int> getBiggestThree(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<vector<int>> s1(m + 1, vector<int>(n + 2)); vector<vector<int>> s2(m + 1, vector<int>(n + 2)); for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1]; s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1]; } } set<int> ss; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { int l = min({i - 1, m - i, j - 1, n - j}); ss.insert(grid[i - 1][j - 1]); for (int k = 1; k <= l; ++k) { int a = s1[i + k][j] - s1[i][j - k]; int b = s1[i][j + k] - s1[i - k][j]; int c = s2[i][j - k] - s2[i - k][j]; int d = s2[i + k][j] - s2[i][j + k]; ss.insert(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]); } while (ss.size() > 3) { ss.erase(ss.begin()); } } } return vector<int>(ss.rbegin(), ss.rend()); } }; -
from sortedcontainers import SortedSet class Solution: def getBiggestThree(self, grid: List[List[int]]) -> List[int]: m, n = len(grid), len(grid[0]) s1 = [[0] * (n + 2) for _ in range(m + 1)] s2 = [[0] * (n + 2) for _ in range(m + 1)] for i, row in enumerate(grid, 1): for j, x in enumerate(row, 1): s1[i][j] = s1[i - 1][j - 1] + x s2[i][j] = s2[i - 1][j + 1] + x ss = SortedSet() for i, row in enumerate(grid, 1): for j, x in enumerate(row, 1): l = min(i - 1, m - i, j - 1, n - j) ss.add(x) for k in range(1, l + 1): a = s1[i + k][j] - s1[i][j - k] b = s1[i][j + k] - s1[i - k][j] c = s2[i][j - k] - s2[i - k][j] d = s2[i + k][j] - s2[i][j + k] ss.add( a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1] ) while len(ss) > 3: ss.remove(ss[0]) return list(ss)[::-1] -
func getBiggestThree(grid [][]int) []int { m, n := len(grid), len(grid[0]) s1 := make([][]int, m+1) s2 := make([][]int, m+1) for i := range s1 { s1[i] = make([]int, n+2) s2[i] = make([]int, n+2) } for i := 1; i <= m; i++ { for j := 1; j <= n; j++ { s1[i][j] = s1[i-1][j-1] + grid[i-1][j-1] s2[i][j] = s2[i-1][j+1] + grid[i-1][j-1] } } ss := treemap.NewWithIntComparator() for i := 1; i <= m; i++ { for j := 1; j <= n; j++ { l := min(i-1, m-i, j-1, n-j) ss.Put(grid[i-1][j-1], nil) for k := 1; k <= l; k++ { a := s1[i+k][j] - s1[i][j-k] b := s1[i][j+k] - s1[i-k][j] c := s2[i][j-k] - s2[i-k][j] d := s2[i+k][j] - s2[i][j+k] ss.Put(a+b+c+d-grid[i+k-1][j-1]+grid[i-k-1][j-1], nil) } for ss.Size() > 3 { x, _ := ss.Min() ss.Remove(x.(int)) } } } ans := make([]int, ss.Size()) for i, k := range ss.Keys() { ans[len(ans)-i-1] = k.(int) } return ans } -
function getBiggestThree(grid: number[][]): number[] { const m = grid.length; const n = grid[0].length; const s1: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0)); const s2: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0)); for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1]; s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1]; } } const ss = new TreeSet<number>(); for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { const l = Math.min(i - 1, m - i, j - 1, n - j); ss.add(grid[i - 1][j - 1]); for (let k = 1; k <= l; ++k) { const a = s1[i + k][j] - s1[i][j - k]; const b = s1[i][j + k] - s1[i - k][j]; const c = s2[i][j - k] - s2[i - k][j]; const d = s2[i + k][j] - s2[i][j + k]; ss.add(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]); } while (ss.size() > 3) { ss.shift(); } } } return [...ss].reverse(); } type Compare<T> = (lhs: T, rhs: T) => number; class RBTreeNode<T = number> { data: T; count: number; left: RBTreeNode<T> | null; right: RBTreeNode<T> | null; parent: RBTreeNode<T> | null; color: number; constructor(data: T) { this.data = data; this.left = this.right = this.parent = null; this.color = 0; this.count = 1; } sibling(): RBTreeNode<T> | null { if (!this.parent) return null; // sibling null if no parent return this.isOnLeft() ? this.parent.right : this.parent.left; } isOnLeft(): boolean { return this === this.parent!.left; } hasRedChild(): boolean { return ( Boolean(this.left && this.left.color === 0) || Boolean(this.right && this.right.color === 0) ); } } class RBTree<T> { root: RBTreeNode<T> | null; lt: (l: T, r: T) => boolean; constructor(compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0)) { this.root = null; this.lt = (l: T, r: T) => compare(l, r) < 0; } rotateLeft(pt: RBTreeNode<T>): void { const right = pt.right!; pt.right = right.left; if (pt.right) pt.right.parent = pt; right.parent = pt.parent; if (!pt.parent) this.root = right; else if (pt === pt.parent.left) pt.parent.left = right; else pt.parent.right = right; right.left = pt; pt.parent = right; } rotateRight(pt: RBTreeNode<T>): void { const left = pt.left!; pt.left = left.right; if (pt.left) pt.left.parent = pt; left.parent = pt.parent; if (!pt.parent) this.root = left; else if (pt === pt.parent.left) pt.parent.left = left; else pt.parent.right = left; left.right = pt; pt.parent = left; } swapColor(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void { const tmp = p1.color; p1.color = p2.color; p2.color = tmp; } swapData(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void { const tmp = p1.data; p1.data = p2.data; p2.data = tmp; } fixAfterInsert(pt: RBTreeNode<T>): void { let parent = null; let grandParent = null; while (pt !== this.root && pt.color !== 1 && pt.parent?.color === 0) { parent = pt.parent; grandParent = pt.parent.parent; /* Case : A Parent of pt is left child of Grand-parent of pt */ if (parent === grandParent?.left) { const uncle = grandParent.right; /* Case : 1 The uncle of pt is also red Only Recoloring required */ if (uncle && uncle.color === 0) { grandParent.color = 0; parent.color = 1; uncle.color = 1; pt = grandParent; } else { /* Case : 2 pt is right child of its parent Left-rotation required */ if (pt === parent.right) { this.rotateLeft(parent); pt = parent; parent = pt.parent; } /* Case : 3 pt is left child of its parent Right-rotation required */ this.rotateRight(grandParent); this.swapColor(parent!, grandParent); pt = parent!; } } else { /* Case : B Parent of pt is right child of Grand-parent of pt */ const uncle = grandParent!.left; /* Case : 1 The uncle of pt is also red Only Recoloring required */ if (uncle != null && uncle.color === 0) { grandParent!.color = 0; parent.color = 1; uncle.color = 1; pt = grandParent!; } else { /* Case : 2 pt is left child of its parent Right-rotation required */ if (pt === parent.left) { this.rotateRight(parent); pt = parent; parent = pt.parent; } /* Case : 3 pt is right child of its parent Left-rotation required */ this.rotateLeft(grandParent!); this.swapColor(parent!, grandParent!); pt = parent!; } } } this.root!.color = 1; } delete(val: T): boolean { const node = this.find(val); if (!node) return false; node.count--; if (!node.count) this.deleteNode(node); return true; } deleteAll(val: T): boolean { const node = this.find(val); if (!node) return false; this.deleteNode(node); return true; } deleteNode(v: RBTreeNode<T>): void { const u = BSTreplace(v); // True when u and v are both black const uvBlack = (u === null || u.color === 1) && v.color === 1; const parent = v.parent!; if (!u) { // u is null therefore v is leaf if (v === this.root) this.root = null; // v is root, making root null else { if (uvBlack) { // u and v both black // v is leaf, fix double black at v this.fixDoubleBlack(v); } else { // u or v is red if (v.sibling()) { // sibling is not null, make it red" v.sibling()!.color = 0; } } // delete v from the tree if (v.isOnLeft()) parent.left = null; else parent.right = null; } return; } if (!v.left || !v.right) { // v has 1 child if (v === this.root) { // v is root, assign the value of u to v, and delete u v.data = u.data; v.left = v.right = null; } else { // Detach v from tree and move u up if (v.isOnLeft()) parent.left = u; else parent.right = u; u.parent = parent; if (uvBlack) this.fixDoubleBlack(u); // u and v both black, fix double black at u else u.color = 1; // u or v red, color u black } return; } // v has 2 children, swap data with successor and recurse this.swapData(u, v); this.deleteNode(u); // find node that replaces a deleted node in BST function BSTreplace(x: RBTreeNode<T>): RBTreeNode<T> | null { // when node have 2 children if (x.left && x.right) return successor(x.right); // when leaf if (!x.left && !x.right) return null; // when single child return x.left ?? x.right; } // find node that do not have a left child // in the subtree of the given node function successor(x: RBTreeNode<T>): RBTreeNode<T> { let temp = x; while (temp.left) temp = temp.left; return temp; } } fixDoubleBlack(x: RBTreeNode<T>): void { if (x === this.root) return; // Reached root const sibling = x.sibling(); const parent = x.parent!; if (!sibling) { // No sibiling, double black pushed up this.fixDoubleBlack(parent); } else { if (sibling.color === 0) { // Sibling red parent.color = 0; sibling.color = 1; if (sibling.isOnLeft()) this.rotateRight(parent); // left case else this.rotateLeft(parent); // right case this.fixDoubleBlack(x); } else { // Sibling black if (sibling.hasRedChild()) { // at least 1 red children if (sibling.left && sibling.left.color === 0) { if (sibling.isOnLeft()) { // left left sibling.left.color = sibling.color; sibling.color = parent.color; this.rotateRight(parent); } else { // right left sibling.left.color = parent.color; this.rotateRight(sibling); this.rotateLeft(parent); } } else { if (sibling.isOnLeft()) { // left right sibling.right!.color = parent.color; this.rotateLeft(sibling); this.rotateRight(parent); } else { // right right sibling.right!.color = sibling.color; sibling.color = parent.color; this.rotateLeft(parent); } } parent.color = 1; } else { // 2 black children sibling.color = 0; if (parent.color === 1) this.fixDoubleBlack(parent); else parent.color = 1; } } } } insert(data: T): boolean { // search for a position to insert let parent = this.root; while (parent) { if (this.lt(data, parent.data)) { if (!parent.left) break; else parent = parent.left; } else if (this.lt(parent.data, data)) { if (!parent.right) break; else parent = parent.right; } else break; } // insert node into parent const node = new RBTreeNode(data); if (!parent) this.root = node; else if (this.lt(node.data, parent.data)) parent.left = node; else if (this.lt(parent.data, node.data)) parent.right = node; else { parent.count++; return false; } node.parent = parent; this.fixAfterInsert(node); return true; } find(data: T): RBTreeNode<T> | null { let p = this.root; while (p) { if (this.lt(data, p.data)) { p = p.left; } else if (this.lt(p.data, data)) { p = p.right; } else break; } return p ?? null; } *inOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> { if (!root) return; for (const v of this.inOrder(root.left!)) yield v; yield root.data; for (const v of this.inOrder(root.right!)) yield v; } *reverseInOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> { if (!root) return; for (const v of this.reverseInOrder(root.right!)) yield v; yield root.data; for (const v of this.reverseInOrder(root.left!)) yield v; } } class TreeSet<T = number> { _size: number; tree: RBTree<T>; compare: Compare<T>; constructor( collection: T[] | Compare<T> = [], compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0), ) { if (typeof collection === 'function') { compare = collection; collection = []; } this._size = 0; this.compare = compare; this.tree = new RBTree(compare); for (const val of collection) this.add(val); } size(): number { return this._size; } has(val: T): boolean { return !!this.tree.find(val); } add(val: T): boolean { const successful = this.tree.insert(val); this._size += successful ? 1 : 0; return successful; } delete(val: T): boolean { const deleted = this.tree.deleteAll(val); this._size -= deleted ? 1 : 0; return deleted; } ceil(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(p.data, val) >= 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } floor(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(val, p.data) >= 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } higher(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(val, p.data) < 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } lower(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(p.data, val) < 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } first(): T | undefined { return this.tree.inOrder().next().value; } last(): T | undefined { return this.tree.reverseInOrder().next().value; } shift(): T | undefined { const first = this.first(); if (first === undefined) return undefined; this.delete(first); return first; } pop(): T | undefined { const last = this.last(); if (last === undefined) return undefined; this.delete(last); return last; } *[Symbol.iterator](): Generator<T, void, void> { for (const val of this.values()) yield val; } *keys(): Generator<T, void, void> { for (const val of this.values()) yield val; } *values(): Generator<T, undefined, void> { for (const val of this.tree.inOrder()) yield val; return undefined; } /** * Return a generator for reverse order traversing the set */ *rvalues(): Generator<T, undefined, void> { for (const val of this.tree.reverseInOrder()) yield val; return undefined; } } class TreeMultiSet<T = number> { _size: number; tree: RBTree<T>; compare: Compare<T>; constructor( collection: T[] | Compare<T> = [], compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0), ) { if (typeof collection === 'function') { compare = collection; collection = []; } this._size = 0; this.compare = compare; this.tree = new RBTree(compare); for (const val of collection) this.add(val); } size(): number { return this._size; } has(val: T): boolean { return !!this.tree.find(val); } add(val: T): boolean { const successful = this.tree.insert(val); this._size++; return successful; } delete(val: T): boolean { const successful = this.tree.delete(val); if (!successful) return false; this._size--; return true; } count(val: T): number { const node = this.tree.find(val); return node ? node.count : 0; } ceil(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(p.data, val) >= 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } floor(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(val, p.data) >= 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } higher(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(val, p.data) < 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } lower(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(p.data, val) < 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } first(): T | undefined { return this.tree.inOrder().next().value; } last(): T | undefined { return this.tree.reverseInOrder().next().value; } shift(): T | undefined { const first = this.first(); if (first === undefined) return undefined; this.delete(first); return first; } pop(): T | undefined { const last = this.last(); if (last === undefined) return undefined; this.delete(last); return last; } *[Symbol.iterator](): Generator<T, void, void> { yield* this.values(); } *keys(): Generator<T, void, void> { for (const val of this.values()) yield val; } *values(): Generator<T, undefined, void> { for (const val of this.tree.inOrder()) { let count = this.count(val); while (count--) yield val; } return undefined; } /** * Return a generator for reverse order traversing the multi-set */ *rvalues(): Generator<T, undefined, void> { for (const val of this.tree.reverseInOrder()) { let count = this.count(val); while (count--) yield val; } return undefined; } }