Welcome to Subscribe On Youtube
1840. Maximum Building Height
Description
You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.
However, there are city restrictions on the heights of the new buildings:
- The height of each building must be a non-negative integer.
- The height of the first building must be
0. - The height difference between any two adjacent buildings cannot exceed
1.
Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.
It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.
Return the maximum possible height of the tallest building.
Example 1:
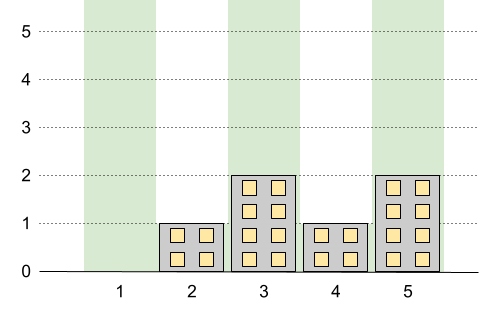
Input: n = 5, restrictions = [[2,1],[4,1]] Output: 2 Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.
Example 2:
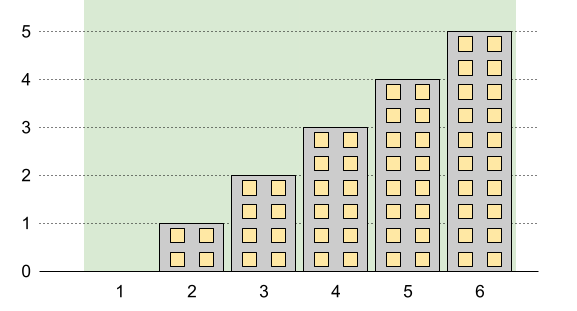
Input: n = 6, restrictions = [] Output: 5 Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.
Example 3:
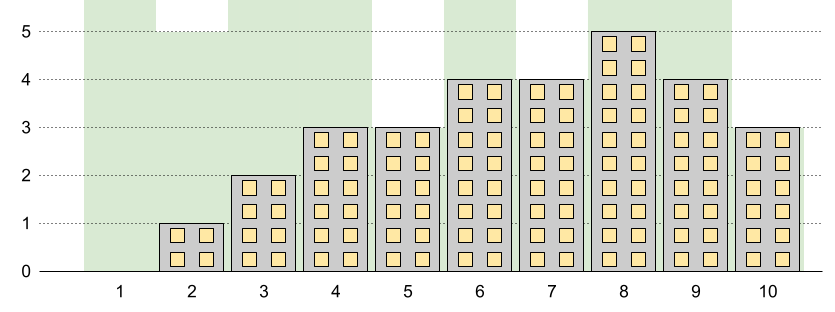
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]] Output: 5 Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.
Constraints:
2 <= n <= 1090 <= restrictions.length <= min(n - 1, 105)2 <= idi <= nidiis unique.0 <= maxHeighti <= 109
Solutions
Soution 1: Sorting + Mathematics
First, we sort all the restrictions by the building number in ascending order.
Then we traverse all the restrictions from left to right. For each restriction, we can get an upper bound of the maximum height, that is, $r_i[1] = \min(r_i[1], r_{i-1}[1] + r_i[0] - r_{i-1}[0])$, where $r_i$ represents the $i$-th restriction, and $r_i[0]$ and $r_i[1]$ represent the building number and the upper bound of the maximum height of the building, respectively.
Then we traverse all the restrictions from right to left. For each restriction, we can get an upper bound of the maximum height, that is, $r_i[1] = \min(r_i[1], r_{i+1}[1] + r_{i+1}[0] - r_i[0])$.
In this way, we get the upper bound of the maximum height for each restricted building.
The problem asks for the height of the tallest building. We can enumerate the buildings $i$ and $i+1$ between two adjacent restrictions. To maximize the height, the height should first increase and then decrease. Suppose the maximum height is $t$, then $t - r_i[1] + t - r_{i+1}[1] \leq r_{i+1}[0] - r_i[0]$, that is, $t \leq \frac{r_i[1] + r_{i+1}[1] + r_{i+1}[0] - r_{i}[0]}{2}$. We can take the maximum value among all $t$.
The time complexity is $O(m \times \log m)$, and the space complexity is $O(m)$. Where $m$ is the number of restrictions.
-
class Solution { public int maxBuilding(int n, int[][] restrictions) { List<int[]> r = new ArrayList<>(); r.addAll(Arrays.asList(restrictions)); r.add(new int[] {1, 0}); Collections.sort(r, (a, b) -> a[0] - b[0]); if (r.get(r.size() - 1)[0] != n) { r.add(new int[] {n, n - 1}); } int m = r.size(); for (int i = 1; i < m; ++i) { int[] a = r.get(i - 1), b = r.get(i); b[1] = Math.min(b[1], a[1] + b[0] - a[0]); } for (int i = m - 2; i > 0; --i) { int[] a = r.get(i), b = r.get(i + 1); a[1] = Math.min(a[1], b[1] + b[0] - a[0]); } int ans = 0; for (int i = 0; i < m - 1; ++i) { int[] a = r.get(i), b = r.get(i + 1); int t = (a[1] + b[1] + b[0] - a[0]) / 2; ans = Math.max(ans, t); } return ans; } } -
class Solution { public: int maxBuilding(int n, vector<vector<int>>& restrictions) { auto&& r = restrictions; r.push_back({1, 0}); sort(r.begin(), r.end()); if (r[r.size() - 1][0] != n) r.push_back({n, n - 1}); int m = r.size(); for (int i = 1; i < m; ++i) { r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0]); } for (int i = m - 2; i > 0; --i) { r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0]); } int ans = 0; for (int i = 0; i < m - 1; ++i) { int t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) / 2; ans = max(ans, t); } return ans; } }; -
class Solution: def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int: r = restrictions r.append([1, 0]) r.sort() if r[-1][0] != n: r.append([n, n - 1]) m = len(r) for i in range(1, m): r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0]) for i in range(m - 2, 0, -1): r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0]) ans = 0 for i in range(m - 1): t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2 ans = max(ans, t) return ans -
func maxBuilding(n int, restrictions [][]int) (ans int) { r := restrictions r = append(r, []int{1, 0}) sort.Slice(r, func(i, j int) bool { return r[i][0] < r[j][0] }) if r[len(r)-1][0] != n { r = append(r, []int{n, n - 1}) } m := len(r) for i := 1; i < m; i++ { r[i][1] = min(r[i][1], r[i-1][1]+r[i][0]-r[i-1][0]) } for i := m - 2; i > 0; i-- { r[i][1] = min(r[i][1], r[i+1][1]+r[i+1][0]-r[i][0]) } for i := 0; i < m-1; i++ { t := (r[i][1] + r[i+1][1] + r[i+1][0] - r[i][0]) / 2 ans = max(ans, t) } return ans }