Welcome to Subscribe On Youtube

1828. Queries on Number of Points Inside a Circle

Description

You are given an array points where points[i] = [xi, yi] is the coordinates of the ith point on a 2D plane. Multiple points can have the same coordinates.

You are also given an array queries where queries[j] = [xj, yj, rj] describes a circle centered at (xj, yj) with a radius of rj.

For each query queries[j], compute the number of points inside the jth circle. Points on the border of the circle are considered inside.

Return an array answer, where answer[j] is the answer to the jth query.

 

Example 1:

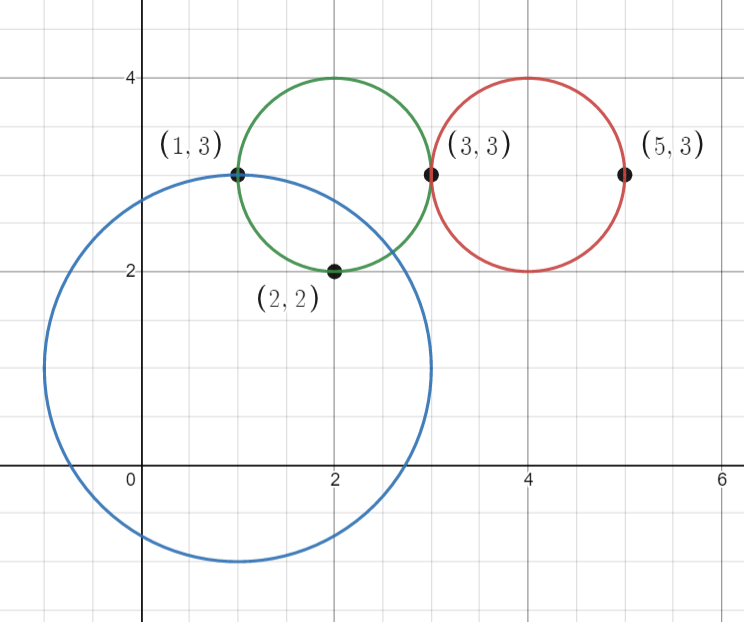
Input: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
Output: [3,2,2]
Explanation: The points and circles are shown above.
queries[0] is the green circle, queries[1] is the red circle, and queries[2] is the blue circle.

Example 2:

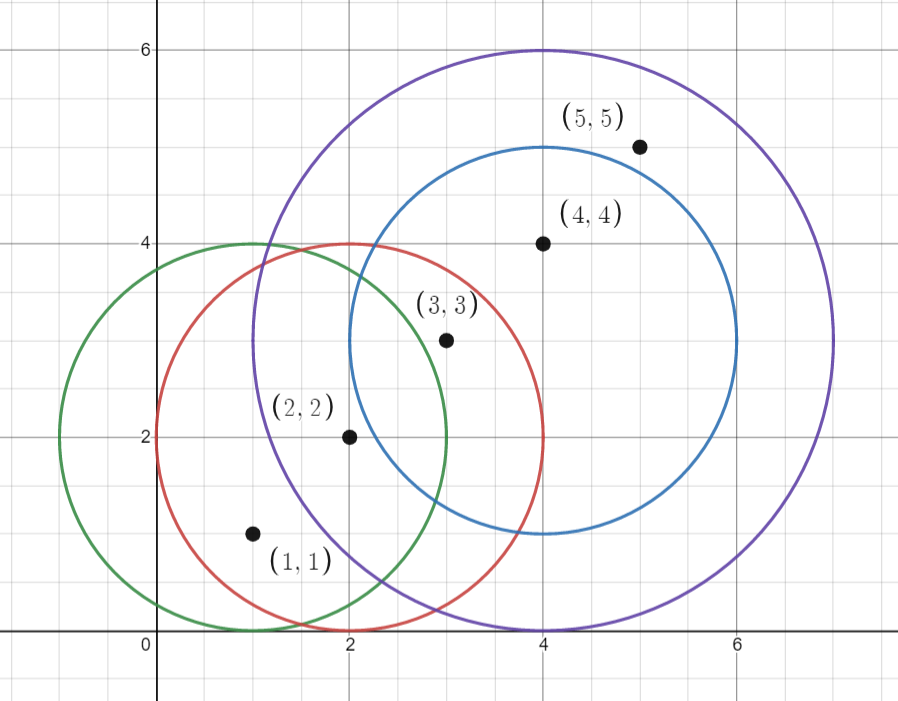
Input: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
Output: [2,3,2,4]
Explanation: The points and circles are shown above.
queries[0] is green, queries[1] is red, queries[2] is blue, and queries[3] is purple.

 

Constraints:

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= x​​​​​​i, y​​​​​​i <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= xj, yj <= 500
• 1 <= rj <= 500
• All coordinates are integers.

 

Follow up: Could you find the answer for each query in better complexity than O(n)?

Solutions

Solution 1: Enumeration

Enumerate all the circles $(x, y, r)$. For each circle, calculate the number of points within the circle to get the answer.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the lengths of the arrays queries and points respectively. Ignoring the space consumption of the answer, the space complexity is $O(1)$.

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public int[] countPoints(int[][] points, int[][] queries) {
          int m = queries.length;
          int[] ans = new int[m];
          for (int k = 0; k < m; ++k) {
              int x = queries[k][0], y = queries[k][1], r = queries[k][2];
              for (var p : points) {
                  int i = p[0], j = p[1];
                  int dx = i - x, dy = j - y;
                  if (dx * dx + dy * dy <= r * r) {
                      ++ans[k];
                  }
              }
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {
          vector<int> ans;
          for (auto& q : queries) {
              int x = q[0], y = q[1], r = q[2];
              int cnt = 0;
              for (auto& p : points) {
                  int i = p[0], j = p[1];
                  int dx = i - x, dy = j - y;
                  cnt += dx * dx + dy * dy <= r * r;
              }
              ans.emplace_back(cnt);
          }
          return ans;
      }
  };
  

• class Solution:
      def countPoints(
          self, points: List[List[int]], queries: List[List[int]]
      ) -> List[int]:
          ans = []
          for x, y, r in queries:
              cnt = 0
              for i, j in points:
                  dx, dy = i - x, j - y
                  cnt += dx * dx + dy * dy <= r * r
              ans.append(cnt)
          return ans
  
  

• func countPoints(points [][]int, queries [][]int) (ans []int) {
  	for _, q := range queries {
  		x, y, r := q[0], q[1], q[2]
  		cnt := 0
  		for _, p := range points {
  			i, j := p[0], p[1]
  			dx, dy := i-x, j-y
  			if dx*dx+dy*dy <= r*r {
  				cnt++
  			}
  		}
  		ans = append(ans, cnt)
  	}
  	return
  }
  

• function countPoints(points: number[][], queries: number[][]): number[] {
      return queries.map(([cx, cy, r]) => {
          let res = 0;
          for (const [px, py] of points) {
              if (Math.sqrt((cx - px) ** 2 + (cy - py) ** 2) <= r) {
                  res++;
              }
          }
          return res;
      });
  }
  
  

• impl Solution {
      pub fn count_points(points: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {
          queries
              .iter()
              .map(|v| {
                  let cx = v[0];
                  let cy = v[1];
                  let r = v[2].pow(2);
                  let mut count = 0;
                  for p in points.iter() {
                      if (p[0] - cx).pow(2) + (p[1] - cy).pow(2) <= r {
                          count += 1;
                      }
                  }
                  count
              })
              .collect()
      }
  }
  
  

All Problems

All Solutions