Welcome to Subscribe On Youtube
1819. Number of Different Subsequences GCDs
Description
You are given an array nums that consists of positive integers.
The GCD of a sequence of numbers is defined as the greatest integer that divides all the numbers in the sequence evenly.
- For example, the GCD of the sequence
[4,6,16]is2.
A subsequence of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
- For example,
[2,5,10]is a subsequence of[1,2,1,2,4,1,5,10].
Return the number of different GCDs among all non-empty subsequences of nums.
Example 1:
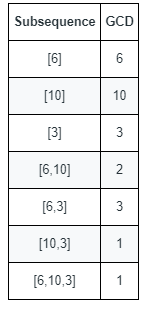
Input: nums = [6,10,3] Output: 5 Explanation: The figure shows all the non-empty subsequences and their GCDs. The different GCDs are 6, 10, 3, 2, and 1.
Example 2:
Input: nums = [5,15,40,5,6] Output: 7
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 2 * 105
Solutions
Solution 1: Enumeration + Mathematics
For all sub-sequences of the array $nums$, their greatest common divisor (GCD) will not exceed the maximum value $mx$ in the array.
Therefore, we can enumerate each number $x$ in $[1,.. mx]$, and determine whether $x$ is the GCD of a sub-sequence of the array $nums$. If it is, then we increment the answer by one.
So the problem is transformed into: determining whether $x$ is the GCD of a sub-sequence of the array $nums$. We can do this by enumerating the multiples $y$ of $x$, and checking whether $y$ exists in the array $nums$. If $y$ exists in the array $nums$, then we calculate the GCD $g$ of $y$. If $g = x$ occurs, then $x$ is the GCD of a sub-sequence of the array $nums$.
The time complexity is $O(n + M \times \log M)$, and the space complexity is $O(M)$. Here, $n$ and $M$ are the length of the array $nums$ and the maximum value in the array $nums$, respectively.
-
class Solution { public int countDifferentSubsequenceGCDs(int[] nums) { int mx = Arrays.stream(nums).max().getAsInt(); boolean[] vis = new boolean[mx + 1]; for (int x : nums) { vis[x] = true; } int ans = 0; for (int x = 1; x <= mx; ++x) { int g = 0; for (int y = x; y <= mx; y += x) { if (vis[y]) { g = gcd(g, y); if (x == g) { ++ans; break; } } } } return ans; } private int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } } -
class Solution { public: int countDifferentSubsequenceGCDs(vector<int>& nums) { int mx = *max_element(nums.begin(), nums.end()); vector<bool> vis(mx + 1); for (int& x : nums) { vis[x] = true; } int ans = 0; for (int x = 1; x <= mx; ++x) { int g = 0; for (int y = x; y <= mx; y += x) { if (vis[y]) { g = gcd(g, y); if (g == x) { ++ans; break; } } } } return ans; } }; -
class Solution: def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int: mx = max(nums) vis = set(nums) ans = 0 for x in range(1, mx + 1): g = 0 for y in range(x, mx + 1, x): if y in vis: g = gcd(g, y) if g == x: ans += 1 break return ans -
func countDifferentSubsequenceGCDs(nums []int) (ans int) { mx := slices.Max(nums) vis := make([]bool, mx+1) for _, x := range nums { vis[x] = true } for x := 1; x <= mx; x++ { g := 0 for y := x; y <= mx; y += x { if vis[y] { g = gcd(g, y) if g == x { ans++ break } } } } return } func gcd(a, b int) int { if b == 0 { return a } return gcd(b, a%b) }