Welcome to Subscribe On Youtube

1791. Find Center of Star Graph

Description

There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.

 

Example 1:

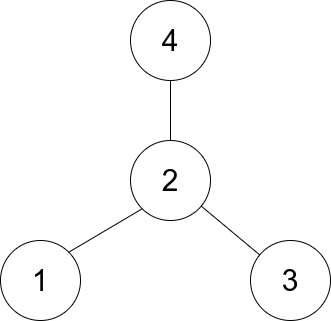
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]]
Output: 1

 

Constraints:

• 3 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ui, vi <= n
• ui != vi
• The given edges represent a valid star graph.

Solutions

Solution 1: Directly Compare the Points of the First Two Edges

The characteristic of the center point is that it is connected to all other points. Therefore, as long as we compare the points of the first two edges, if there are the same points, then this point is the center point.

The time complexity is $O(1)$, and the space complexity is $O(1)$.

• Java
• C++
• Python
• Go
• TypeScript
• Javascript
• RenderScript

• class Solution {
      public int findCenter(int[][] edges) {
          int a = edges[0][0], b = edges[0][1];
          int c = edges[1][0], d = edges[1][1];
          return a == c || a == d ? a : b;
      }
  }
  

• class Solution {
  public:
      int findCenter(vector<vector<int>>& edges) {
          int a = edges[0][0], b = edges[0][1];
          int c = edges[1][0], d = edges[1][1];
          return a == c || a == d ? a : b;
      }
  };
  

• class Solution:
      def findCenter(self, edges: List[List[int]]) -> int:
          return edges[0][0] if edges[0][0] in edges[1] else edges[0][1]
  
  

• func findCenter(edges [][]int) int {
  	a, b := edges[0][0], edges[0][1]
  	c, d := edges[1][0], edges[1][1]
  	if a == c || a == d {
  		return a
  	}
  	return b
  }
  

• function findCenter(edges: number[][]): number {
      for (let num of edges[0]) {
          if (edges[1].includes(num)) {
              return num;
          }
      }
  }
  
  

• /**
   * @param {number[][]} edges
   * @return {number}
   */
  var findCenter = function (edges) {
      const [a, b] = edges[0];
      const [c, d] = edges[1];
      return a == c || a == d ? a : b;
  };
  
  

• impl Solution {
      pub fn find_center(edges: Vec<Vec<i32>>) -> i32 {
          if edges[0][0] == edges[1][0] || edges[0][0] == edges[1][1] {
              return edges[0][0];
          }
          edges[0][1]
      }
  }
  
  

All Problems

All Solutions