Welcome to Subscribe On Youtube
1786. Number of Restricted Paths From First to Last Node
Description
There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [ui, vi, weighti] denotes that there is an edge between nodes ui and vi with weight equal to weighti.
A path from node start to node end is a sequence of nodes [z0, z1, z2, ..., zk] such that z0 = start and zk = end and there is an edge between zi and zi+1 where 0 <= i <= k-1.
The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(zi) > distanceToLastNode(zi+1) where 0 <= i <= k-1.
Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 109 + 7.
Example 1:
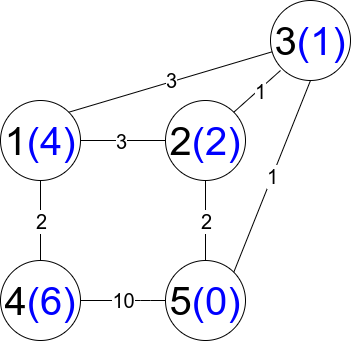
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5
Example 2:
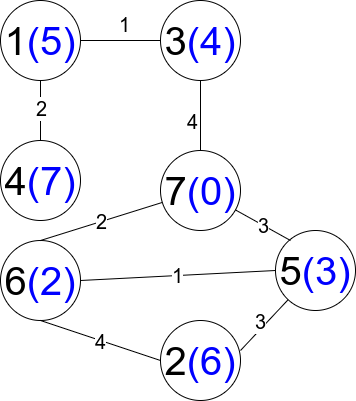
Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The only restricted path is 1 --> 3 --> 7.
Constraints:
1 <= n <= 2 * 104n - 1 <= edges.length <= 4 * 104edges[i].length == 31 <= ui, vi <= nui != vi1 <= weighti <= 105- There is at most one edge between any two nodes.
- There is at least one path between any two nodes.
Solutions
-
class Solution { private static final int INF = Integer.MAX_VALUE; private static final int MOD = (int) 1e9 + 7; private List<int[]>[] g; private int[] dist; private int[] f; private int n; public int countRestrictedPaths(int n, int[][] edges) { this.n = n; g = new List[n + 1]; for (int i = 0; i < g.length; ++i) { g[i] = new ArrayList<>(); } for (int[] e : edges) { int u = e[0], v = e[1], w = e[2]; g[u].add(new int[] {v, w}); g[v].add(new int[] {u, w}); } PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]); q.offer(new int[] {0, n}); dist = new int[n + 1]; f = new int[n + 1]; Arrays.fill(dist, INF); Arrays.fill(f, -1); dist[n] = 0; while (!q.isEmpty()) { int[] p = q.poll(); int u = p[1]; for (int[] ne : g[u]) { int v = ne[0], w = ne[1]; if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; q.offer(new int[] {dist[v], v}); } } } return dfs(1); } private int dfs(int i) { if (f[i] != -1) { return f[i]; } if (i == n) { return 1; } int ans = 0; for (int[] ne : g[i]) { int j = ne[0]; if (dist[i] > dist[j]) { ans = (ans + dfs(j)) % MOD; } } f[i] = ans; return ans; } } -
using pii = pair<int, int>; class Solution { public: const int inf = INT_MAX; const int mod = 1e9 + 7; vector<vector<pii>> g; vector<int> dist; vector<int> f; int n; int countRestrictedPaths(int n, vector<vector<int>>& edges) { this->n = n; g.resize(n + 1); dist.assign(n + 1, inf); f.assign(n + 1, -1); dist[n] = 0; for (auto& e : edges) { int u = e[0], v = e[1], w = e[2]; g[u].emplace_back(v, w); g[v].emplace_back(u, w); } priority_queue<pii, vector<pii>, greater<pii>> q; q.emplace(0, n); while (!q.empty()) { auto [_, u] = q.top(); q.pop(); for (auto [v, w] : g[u]) { if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; q.emplace(dist[v], v); } } } return dfs(1); } int dfs(int i) { if (f[i] != -1) return f[i]; if (i == n) return 1; int ans = 0; for (auto [j, _] : g[i]) { if (dist[i] > dist[j]) { ans = (ans + dfs(j)) % mod; } } f[i] = ans; return ans; } }; -
class Solution: def countRestrictedPaths(self, n: int, edges: List[List[int]]) -> int: @cache def dfs(i): if i == n: return 1 ans = 0 for j, _ in g[i]: if dist[i] > dist[j]: ans = (ans + dfs(j)) % mod return ans g = defaultdict(list) for u, v, w in edges: g[u].append((v, w)) g[v].append((u, w)) q = [(0, n)] dist = [inf] * (n + 1) dist[n] = 0 mod = 10**9 + 7 while q: _, u = heappop(q) for v, w in g[u]: if dist[v] > dist[u] + w: dist[v] = dist[u] + w heappush(q, (dist[v], v)) return dfs(1) -
const inf = math.MaxInt32 const mod = 1e9 + 7 type pair struct { first int second int } var _ heap.Interface = (*pairs)(nil) type pairs []pair func (a pairs) Len() int { return len(a) } func (a pairs) Less(i int, j int) bool { return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second } func (a pairs) Swap(i int, j int) { a[i], a[j] = a[j], a[i] } func (a *pairs) Push(x any) { *a = append(*a, x.(pair)) } func (a *pairs) Pop() any { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t } func countRestrictedPaths(n int, edges [][]int) int { g := make([]pairs, n+1) for _, e := range edges { u, v, w := e[0], e[1], e[2] g[u] = append(g[u], pair{v, w}) g[v] = append(g[v], pair{u, w}) } dist := make([]int, n+1) f := make([]int, n+1) for i := range dist { dist[i] = inf f[i] = -1 } dist[n] = 0 h := make(pairs, 0) heap.Push(&h, pair{0, n}) for len(h) > 0 { u := heap.Pop(&h).(pair).second for _, ne := range g[u] { v, w := ne.first, ne.second if dist[v] > dist[u]+w { dist[v] = dist[u] + w heap.Push(&h, pair{dist[v], v}) } } } var dfs func(int) int dfs = func(i int) int { if f[i] != -1 { return f[i] } if i == n { return 1 } ans := 0 for _, ne := range g[i] { j := ne.first if dist[i] > dist[j] { ans = (ans + dfs(j)) % mod } } f[i] = ans return ans } return dfs(1) }