Welcome to Subscribe On Youtube
1761. Minimum Degree of a Connected Trio in a Graph
Description
You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi.
A connected trio is a set of three nodes where there is an edge between every pair of them.
The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.
Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.
Example 1:
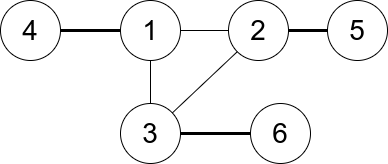
Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]] Output: 3 Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.
Example 2:
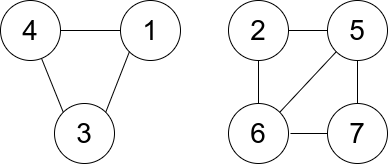
Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]] Output: 0 Explanation: There are exactly three trios: 1) [1,4,3] with degree 0. 2) [2,5,6] with degree 2. 3) [5,6,7] with degree 2.
Constraints:
2 <= n <= 400edges[i].length == 21 <= edges.length <= n * (n-1) / 21 <= ui, vi <= nui != vi- There are no repeated edges.
Solutions
-
class Solution { public int minTrioDegree(int n, int[][] edges) { boolean[][] g = new boolean[n][n]; int[] deg = new int[n]; for (var e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u][v] = true; g[v][u] = true; ++deg[u]; ++deg[v]; } int ans = 1 << 30; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { if (g[i][j]) { for (int k = j + 1; k < n; ++k) { if (g[i][k] && g[j][k]) { ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans == 1 << 30 ? -1 : ans; } } -
class Solution { public: int minTrioDegree(int n, vector<vector<int>>& edges) { bool g[n][n]; memset(g, 0, sizeof g); int deg[n]; memset(deg, 0, sizeof deg); for (auto& e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u][v] = g[v][u] = true; deg[u]++, deg[v]++; } int ans = INT_MAX; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { if (g[i][j]) { for (int k = j + 1; k < n; ++k) { if (g[j][k] && g[i][k]) { ans = min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans == INT_MAX ? -1 : ans; } }; -
class Solution: def minTrioDegree(self, n: int, edges: List[List[int]]) -> int: g = [[False] * n for _ in range(n)] deg = [0] * n for u, v in edges: u, v = u - 1, v - 1 g[u][v] = g[v][u] = True deg[u] += 1 deg[v] += 1 ans = inf for i in range(n): for j in range(i + 1, n): if g[i][j]: for k in range(j + 1, n): if g[i][k] and g[j][k]: ans = min(ans, deg[i] + deg[j] + deg[k] - 6) return -1 if ans == inf else ans -
func minTrioDegree(n int, edges [][]int) int { g := make([][]bool, n) deg := make([]int, n) for i := range g { g[i] = make([]bool, n) } for _, e := range edges { u, v := e[0]-1, e[1]-1 g[u][v], g[v][u] = true, true deg[u]++ deg[v]++ } ans := 1 << 30 for i := 0; i < n; i++ { for j := i + 1; j < n; j++ { if g[i][j] { for k := j + 1; k < n; k++ { if g[i][k] && g[j][k] { ans = min(ans, deg[i]+deg[j]+deg[k]-6) } } } } } if ans == 1<<30 { return -1 } return ans } -
function minTrioDegree(n: number, edges: number[][]): number { const g = Array.from({ length: n }, () => Array(n).fill(false)); const deg: number[] = Array(n).fill(0); for (let [u, v] of edges) { u--; v--; g[u][v] = g[v][u] = true; ++deg[u]; ++deg[v]; } let ans = Infinity; for (let i = 0; i < n; ++i) { for (let j = i + 1; j < n; ++j) { if (g[i][j]) { for (let k = j + 1; k < n; ++k) { if (g[i][k] && g[j][k]) { ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans === Infinity ? -1 : ans; }