Welcome to Subscribe On Youtube

1751. Maximum Number of Events That Can Be Attended II

Description

You are given an array of events where events[i] = [startDayi, endDayi, valuei]. The ith event starts at startDayi and ends at endDayi, and if you attend this event, you will receive a value of valuei. You are also given an integer k which represents the maximum number of events you can attend.

You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.

Return the maximum sum of values that you can receive by attending events.

 

Example 1:

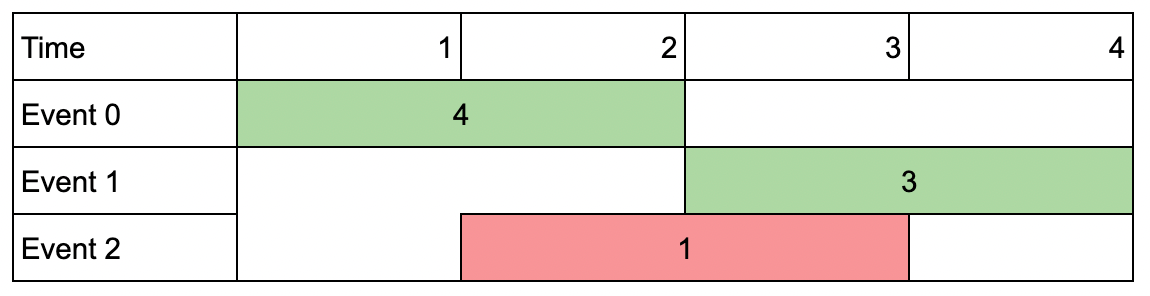
Input: events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output: 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.

Example 2:

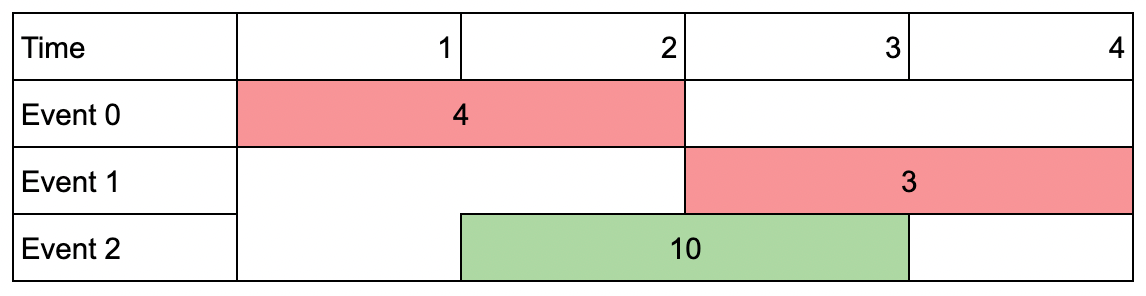
Input: events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output: 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do not have to attend k events.

Example 3:

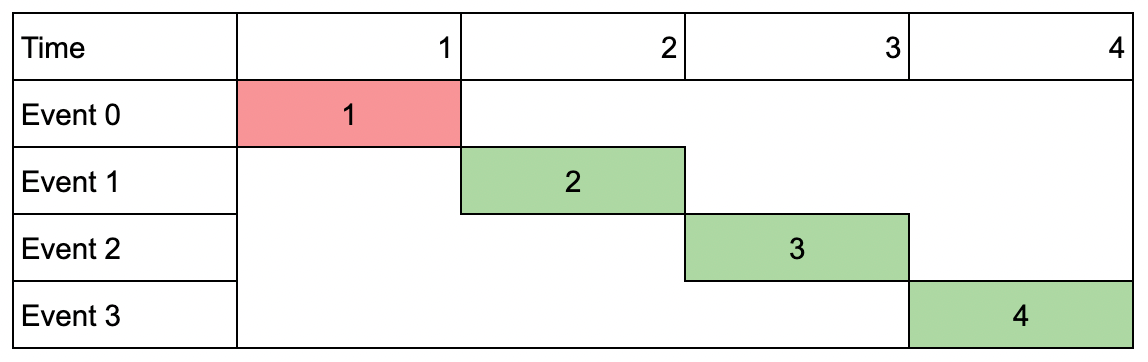
Input: events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output: 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.

 

Constraints:

• 1 <= k <= events.length
• 1 <= k * events.length <= 106
• 1 <= startDayi <= endDayi <= 109
• 1 <= valuei <= 106

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private int[][] events;
      private int[][] f;
      private int n;
  
      public int maxValue(int[][] events, int k) {
          Arrays.sort(events, (a, b) -> a[0] - b[0]);
          this.events = events;
          n = events.length;
          f = new int[n][k + 1];
          return dfs(0, k);
      }
  
      private int dfs(int i, int k) {
          if (i >= n || k <= 0) {
              return 0;
          }
          if (f[i][k] != 0) {
              return f[i][k];
          }
          int j = search(events, events[i][1], i + 1);
          int ans = Math.max(dfs(i + 1, k), dfs(j, k - 1) + events[i][2]);
          return f[i][k] = ans;
      }
  
      private int search(int[][] events, int x, int lo) {
          int l = lo, r = n;
          while (l < r) {
              int mid = (l + r) >> 1;
              if (events[mid][0] > x) {
                  r = mid;
              } else {
                  l = mid + 1;
              }
          }
          return l;
      }
  }
  

• class Solution {
  public:
      int maxValue(vector<vector<int>>& events, int k) {
          sort(events.begin(), events.end());
          int n = events.size();
          int f[n][k + 1];
          memset(f, 0, sizeof(f));
          function<int(int, int)> dfs = [&](int i, int k) -> int {
              if (i >= n || k <= 0) {
                  return 0;
              }
              if (f[i][k] > 0) {
                  return f[i][k];
              }
              int ed = events[i][1], val = events[i][2];
              vector<int> t = {ed};
              int p = upper_bound(events.begin() + i + 1, events.end(), t, [](const auto& a, const auto& b) { return a[0] < b[0]; }) - events.begin();
              f[i][k] = max(dfs(i + 1, k), dfs(p, k - 1) + val);
              return f[i][k];
          };
          return dfs(0, k);
      }
  };
  

• class Solution:
      def maxValue(self, events: List[List[int]], k: int) -> int:
          @cache
          def dfs(i: int, k: int) -> int:
              if i >= len(events):
                  return 0
              _, ed, val = events[i]
              ans = dfs(i + 1, k)
              if k:
                  j = bisect_right(events, ed, lo=i + 1, key=lambda x: x[0])
                  ans = max(ans, dfs(j, k - 1) + val)
              return ans
  
          events.sort()
          return dfs(0, k)
  
  

• func maxValue(events [][]int, k int) int {
  	sort.Slice(events, func(i, j int) bool { return events[i][0] < events[j][0] })
  	n := len(events)
  	f := make([][]int, n)
  	for i := range f {
  		f[i] = make([]int, k+1)
  	}
  	var dfs func(i, k int) int
  	dfs = func(i, k int) int {
  		if i >= n || k <= 0 {
  			return 0
  		}
  		if f[i][k] > 0 {
  			return f[i][k]
  		}
  		j := sort.Search(n, func(h int) bool { return events[h][0] > events[i][1] })
  		ans := max(dfs(i+1, k), dfs(j, k-1)+events[i][2])
  		f[i][k] = ans
  		return ans
  	}
  	return dfs(0, k)
  }
  

• function maxValue(events: number[][], k: number): number {
      events.sort((a, b) => a[1] - b[1]);
      const n = events.length;
      const f: number[][] = new Array(n + 1).fill(0).map(() => new Array(k + 1).fill(0));
      const search = (x: number, hi: number): number => {
          let l = 0;
          let r = hi;
          while (l < r) {
              const mid = (l + r) >> 1;
              if (events[mid][1] >= x) {
                  r = mid;
              } else {
                  l = mid + 1;
              }
          }
          return l;
      };
      for (let i = 1; i <= n; ++i) {
          const [st, _, val] = events[i - 1];
          const p = search(st, i - 1);
          for (let j = 1; j <= k; ++j) {
              f[i][j] = Math.max(f[i - 1][j], f[p][j - 1] + val);
          }
      }
      return f[n][k];
  }
  
  

All Problems

All Solutions