Welcome to Subscribe On Youtube

1728. Cat and Mouse II

Description

A game is played by a cat and a mouse named Cat and Mouse.

The environment is represented by a grid of size rows x cols, where each element is a wall, floor, player (Cat, Mouse), or food.

• Players are represented by the characters 'C'(Cat),'M'(Mouse).
• Floors are represented by the character '.' and can be walked on.
• Walls are represented by the character '#' and cannot be walked on.
• Food is represented by the character 'F' and can be walked on.
• There is only one of each character 'C', 'M', and 'F' in grid.

Mouse and Cat play according to the following rules:

• Mouse moves first, then they take turns to move.
• During each turn, Cat and Mouse can jump in one of the four directions (left, right, up, down). They cannot jump over the wall nor outside of the grid.
• catJump, mouseJump are the maximum lengths Cat and Mouse can jump at a time, respectively. Cat and Mouse can jump less than the maximum length.
• Staying in the same position is allowed.
• Mouse can jump over Cat.

The game can end in 4 ways:

• If Cat occupies the same position as Mouse, Cat wins.
• If Cat reaches the food first, Cat wins.
• If Mouse reaches the food first, Mouse wins.
• If Mouse cannot get to the food within 1000 turns, Cat wins.

Given a rows x cols matrix grid and two integers catJump and mouseJump, return true if Mouse can win the game if both Cat and Mouse play optimally, otherwise return false.

 

Example 1:

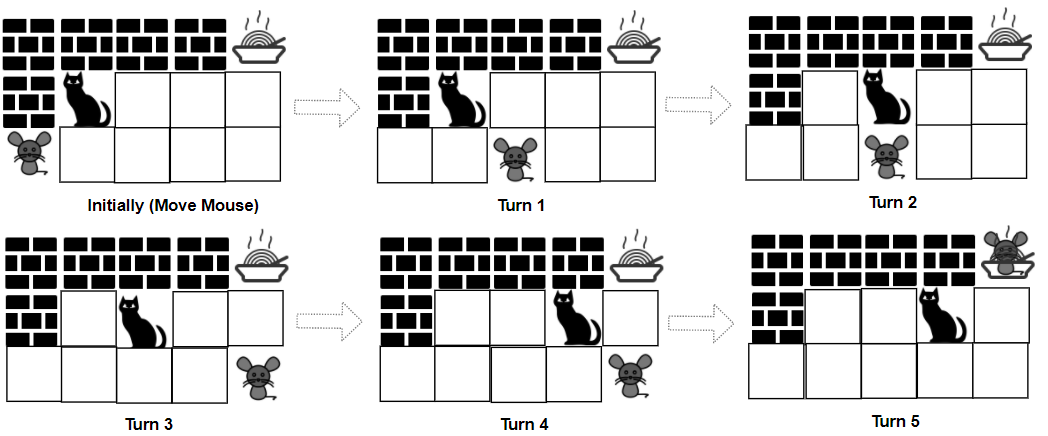
Input: grid = ["####F","#C...","M...."], catJump = 1, mouseJump = 2
Output: true
Explanation: Cat cannot catch Mouse on its turn nor can it get the food before Mouse.

Example 2:

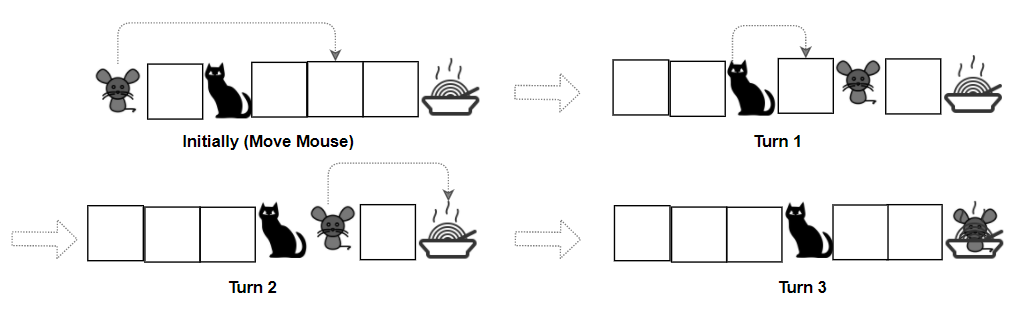
Input: grid = ["M.C...F"], catJump = 1, mouseJump = 4
Output: true

Example 3:

Input: grid = ["M.C...F"], catJump = 1, mouseJump = 3
Output: false

 

Constraints:

• rows == grid.length
• cols = grid[i].length
• 1 <= rows, cols <= 8
• grid[i][j] consist only of characters 'C', 'M', 'F', '.', and '#'.
• There is only one of each character 'C', 'M', and 'F' in grid.
• 1 <= catJump, mouseJump <= 8

Solutions

• Python

• class Solution:
      def canMouseWin(self, grid: List[str], catJump: int, mouseJump: int) -> bool:
          dirs = [0, 1, 0, -1, 0]
          m = len(grid)
          n = len(grid[0])
          nFloors = 0
          cat = 0  # cat's position
          mouse = 0  # mouse's position
  
          def hash(i: int, j: int) -> int:
              return i * n + j
  
          for i in range(m):
              for j in range(n):
                  if grid[i][j] != "#":
                      nFloors += 1
                  if grid[i][j] == "C":
                      cat = hash(i, j)
                  elif grid[i][j] == "M":
                      mouse = hash(i, j)
  
          # dp(i, j, k) := True if mouse can win w//
          # Cat on (i // 8, i % 8), mouse on (j // 8, j % 8), and turns = k
          @functools.lru_cache(None)
          def dp(cat: int, mouse: int, turn: int) -> bool:
              # We already search whole touchable grid
              if turn == nFloors * 2:
                  return False
  
              if turn % 2 == 0:
                  # mouse's turn
                  i = mouse // n
                  j = mouse % n
                  for k in range(4):
                      for jump in range(mouseJump + 1):
                          x = i + dirs[k] * jump
                          y = j + dirs[k + 1] * jump
                          if x < 0 or x == m or y < 0 or y == n:
                              break
                          if grid[x][y] == "#":
                              break
                          if grid[x][y] == "F":  # Mouse eats the food, so mouse win
                              return True
                          if dp(cat, hash(x, y), turn + 1):
                              return True
                  # Mouse can't win, so mouse lose
                  return False
              else:
                  # cat's turn
                  i = cat // n
                  j = cat % n
                  for k in range(4):
                      for jump in range(catJump + 1):
                          x = i + dirs[k] * jump
                          y = j + dirs[k + 1] * jump
                          if x < 0 or x == m or y < 0 or y == n:
                              break
                          if grid[x][y] == "#":
                              break
                          if grid[x][y] == "F":  # Cat eats the food, so mouse lose
                              return False
                          nextCat = hash(x, y)
                          if nextCat == mouse:  # Cat catches mouse, so mouse lose
                              return False
                          if not dp(nextCat, mouse, turn + 1):
                              return False
                  # Cat can't win, so mouse win
                  return True
  
          return dp(cat, mouse, 0)
  
  

All Problems

All Solutions