Welcome to Subscribe On Youtube
1637. Widest Vertical Area Between Two Points Containing No Points
Description
Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.
A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.
Note that points on the edge of a vertical area are not considered included in the area.
Example 1:
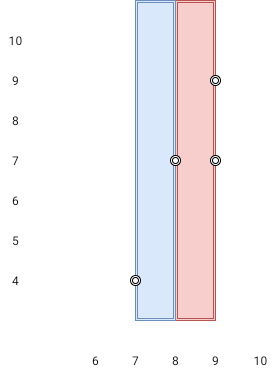
Input: points = [[8,7],[9,9],[7,4],[9,7]] Output: 1 Explanation: Both the red and the blue area are optimal.
Example 2:
Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]] Output: 3
Constraints:
n == points.length2 <= n <= 105points[i].length == 20 <= xi, yi <= 109
Solutions
-
class Solution { public int maxWidthOfVerticalArea(int[][] points) { Arrays.sort(points, (a, b) -> a[0] - b[0]); int ans = 0; for (int i = 0; i < points.length - 1; ++i) { ans = Math.max(ans, points[i + 1][0] - points[i][0]); } return ans; } } -
class Solution { public: int maxWidthOfVerticalArea(vector<vector<int>>& points) { sort(points.begin(), points.end()); int ans = 0; for (int i = 0; i < points.size() - 1; ++i) { ans = max(ans, points[i + 1][0] - points[i][0]); } return ans; } }; -
class Solution: def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int: points.sort() return max(b[0] - a[0] for a, b in pairwise(points)) -
func maxWidthOfVerticalArea(points [][]int) (ans int) { sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] }) for i, p := range points[1:] { ans = max(ans, p[0]-points[i][0]) } return } -
function maxWidthOfVerticalArea(points: number[][]): number { points.sort((a, b) => a[0] - b[0]); let ans = 0; for (let i = 1; i < points.length; ++i) { ans = Math.max(ans, points[i][0] - points[i - 1][0]); } return ans; } -
/** * @param {number[][]} points * @return {number} */ var maxWidthOfVerticalArea = function (points) { points.sort((a, b) => a[0] - b[0]); let ans = 0; let px = points[0][0]; for (const [x, _] of points) { ans = Math.max(ans, x - px); px = x; } return ans; };