Welcome to Subscribe On Youtube
1621. Number of Sets of K Non-Overlapping Line Segments
Description
Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.
Return the number of ways we can draw k non-overlapping line segments. Since this number can be huge, return it modulo 109 + 7.
Example 1:
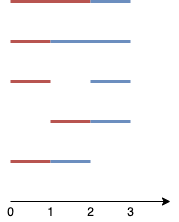
Input: n = 4, k = 2
Output: 5
Explanation: The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.
Example 2:
Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.
Example 3:
Input: n = 30, k = 7 Output: 796297179 Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.
Constraints:
2 <= n <= 10001 <= k <= n-1
Solutions
-
class Solution { private static final int MOD = (int) 1e9 + 7; public int numberOfSets(int n, int k) { int[][] f = new int[n + 1][k + 1]; int[][] g = new int[n + 1][k + 1]; f[1][0] = 1; for (int i = 2; i <= n; ++i) { for (int j = 0; j <= k; ++j) { f[i][j] = (f[i - 1][j] + g[i - 1][j]) % MOD; g[i][j] = g[i - 1][j]; if (j > 0) { g[i][j] += f[i - 1][j - 1]; g[i][j] %= MOD; g[i][j] += g[i - 1][j - 1]; g[i][j] %= MOD; } } } return (f[n][k] + g[n][k]) % MOD; } } -
class Solution { public: int f[1010][1010]; int g[1010][1010]; const int mod = 1e9 + 7; int numberOfSets(int n, int k) { memset(f, 0, sizeof(f)); memset(g, 0, sizeof(g)); f[1][0] = 1; for (int i = 2; i <= n; ++i) { for (int j = 0; j <= k; ++j) { f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod; g[i][j] = g[i - 1][j]; if (j > 0) { g[i][j] += f[i - 1][j - 1]; g[i][j] %= mod; g[i][j] += g[i - 1][j - 1]; g[i][j] %= mod; } } } return (f[n][k] + g[n][k]) % mod; } }; -
class Solution: def numberOfSets(self, n: int, k: int) -> int: mod = 10**9 + 7 f = [[0] * (k + 1) for _ in range(n + 1)] g = [[0] * (k + 1) for _ in range(n + 1)] f[1][0] = 1 for i in range(2, n + 1): for j in range(k + 1): f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod g[i][j] = g[i - 1][j] if j: g[i][j] += f[i - 1][j - 1] g[i][j] %= mod g[i][j] += g[i - 1][j - 1] g[i][j] %= mod return (f[-1][-1] + g[-1][-1]) % mod -
func numberOfSets(n int, k int) int { f := make([][]int, n+1) g := make([][]int, n+1) for i := range f { f[i] = make([]int, k+1) g[i] = make([]int, k+1) } f[1][0] = 1 var mod int = 1e9 + 7 for i := 2; i <= n; i++ { for j := 0; j <= k; j++ { f[i][j] = (f[i-1][j] + g[i-1][j]) % mod g[i][j] = g[i-1][j] if j > 0 { g[i][j] += f[i-1][j-1] g[i][j] %= mod g[i][j] += g[i-1][j-1] g[i][j] %= mod } } } return (f[n][k] + g[n][k]) % mod } -
function numberOfSets(n: number, k: number): number { const f = Array.from({ length: n + 1 }, _ => new Array(k + 1).fill(0)); const g = Array.from({ length: n + 1 }, _ => new Array(k + 1).fill(0)); f[1][0] = 1; const mod = 10 ** 9 + 7; for (let i = 2; i <= n; ++i) { for (let j = 0; j <= k; ++j) { f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod; g[i][j] = g[i - 1][j]; if (j) { g[i][j] += f[i - 1][j - 1]; g[i][j] %= mod; g[i][j] += g[i - 1][j - 1]; g[i][j] %= mod; } } } return (f[n][k] + g[n][k]) % mod; }