Welcome to Subscribe On Youtube

1609. Even Odd Tree

Description

A binary tree is named Even-Odd if it meets the following conditions:

• The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
• For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
• For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

 

Example 1:

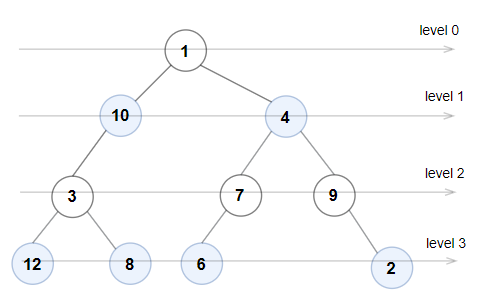
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2:

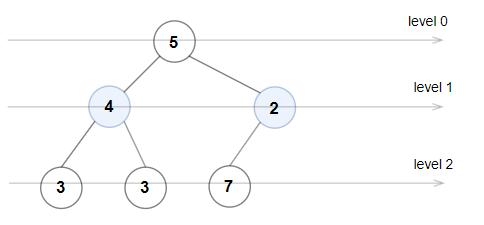
Input: root = [5,4,2,3,3,7]
Output: false
Explanation: The node values on each level are:
Level 0: [5]
Level 1: [4,2]
Level 2: [3,3,7]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3:

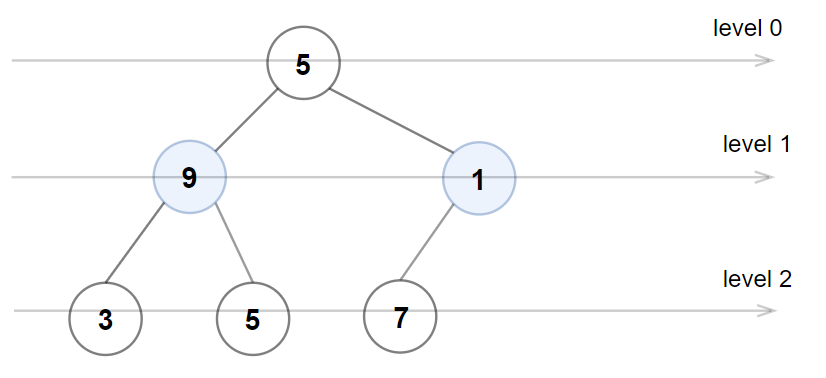
Input: root = [5,9,1,3,5,7]
Output: false
Explanation: Node values in the level 1 should be even integers.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 106

Solutions

BFS.

• Java
• C++
• Python
• Go

• /**
   * Definition for a binary tree node.
   * public class TreeNode {
   * int val;
   * TreeNode left;
   * TreeNode right;
   * TreeNode() {}
   * TreeNode(int val) { this.val = val; }
   * TreeNode(int val, TreeNode left, TreeNode right) {
   * this.val = val;
   * this.left = left;
   * this.right = right;
   * }
   * }
   */
  class Solution {
    public boolean isEvenOddTree(TreeNode root) {
      Queue < TreeNode > que = new LinkedList < > ();
      que.add(root);
      que.add(null);
      int res = 1;
      int c = 0;
      int prev = 0;
      while (!que.isEmpty()) {
        if (res % 2 == 0)
          prev = Integer.MAX_VALUE;
        else
          prev = Integer.MIN_VALUE;
        while (que.peek() != null) {
          if (que.peek().val % 2 != res % 2) {
            return false;
          }
          if (res % 2 == 0 && prev <= que.peek().val) {
            return false;
          }
  
          if (res % 2 != 0 && prev >= que.peek().val)
            return false;
          if (que.peek().left != null)
            que.add(que.peek().left);
          if (que.peek().right != null)
            que.add(que.peek().right);
          prev = que.poll().val;
        }
        que.poll();
        if (que.isEmpty()) {
          break;
        }
        res++;
        que.add(null);
  
      }
      return true;
    }
  }
  

• /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
   *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
   *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
   * };
   */
  class Solution {
  public:
      bool isEvenOddTree(TreeNode* root) {
          int even = 1;
          queue<TreeNode*> q{ {root} };
          while (!q.empty()) {
              int prev = even ? 0 : 1e6;
              for (int n = q.size(); n; --n) {
                  root = q.front();
                  q.pop();
                  if (even && (root->val % 2 == 0 || prev >= root->val)) return false;
                  if (!even && (root->val % 2 == 1 || prev <= root->val)) return false;
                  prev = root->val;
                  if (root->left) q.push(root->left);
                  if (root->right) q.push(root->right);
              }
              even ^= 1;
          }
          return true;
      }
  };
  

• # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right
  class Solution:
      def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
          even = 1
          q = deque([root])
          while q:
              prev = 0 if even else inf
              for _ in range(len(q)):
                  root = q.popleft()
                  if even and (root.val % 2 == 0 or prev >= root.val):
                      return False
                  if not even and (root.val % 2 == 1 or prev <= root.val):
                      return False
                  prev = root.val
                  if root.left:
                      q.append(root.left)
                  if root.right:
                      q.append(root.right)
              even ^= 1
          return True
  
  

• /**
   * Definition for a binary tree node.
   * type TreeNode struct {
   *     Val int
   *     Left *TreeNode
   *     Right *TreeNode
   * }
   */
  func isEvenOddTree(root *TreeNode) bool {
  	even := true
  	q := []*TreeNode{root}
  	for len(q) > 0 {
  		var prev int = 1e6
  		if even {
  			prev = 0
  		}
  		for n := len(q); n > 0; n-- {
  			root = q[0]
  			q = q[1:]
  			if even && (root.Val%2 == 0 || prev >= root.Val) {
  				return false
  			}
  			if !even && (root.Val%2 == 1 || prev <= root.Val) {
  				return false
  			}
  			prev = root.Val
  			if root.Left != nil {
  				q = append(q, root.Left)
  			}
  			if root.Right != nil {
  				q = append(q, root.Right)
  			}
  		}
  		even = !even
  	}
  	return true
  }
  

All Problems

All Solutions