1601. Maximum Number of Achievable Transfer Requests

Description

We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [from_i, to_i] represents an employee's request to transfer from building from_i to building to_i.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

Example 1:

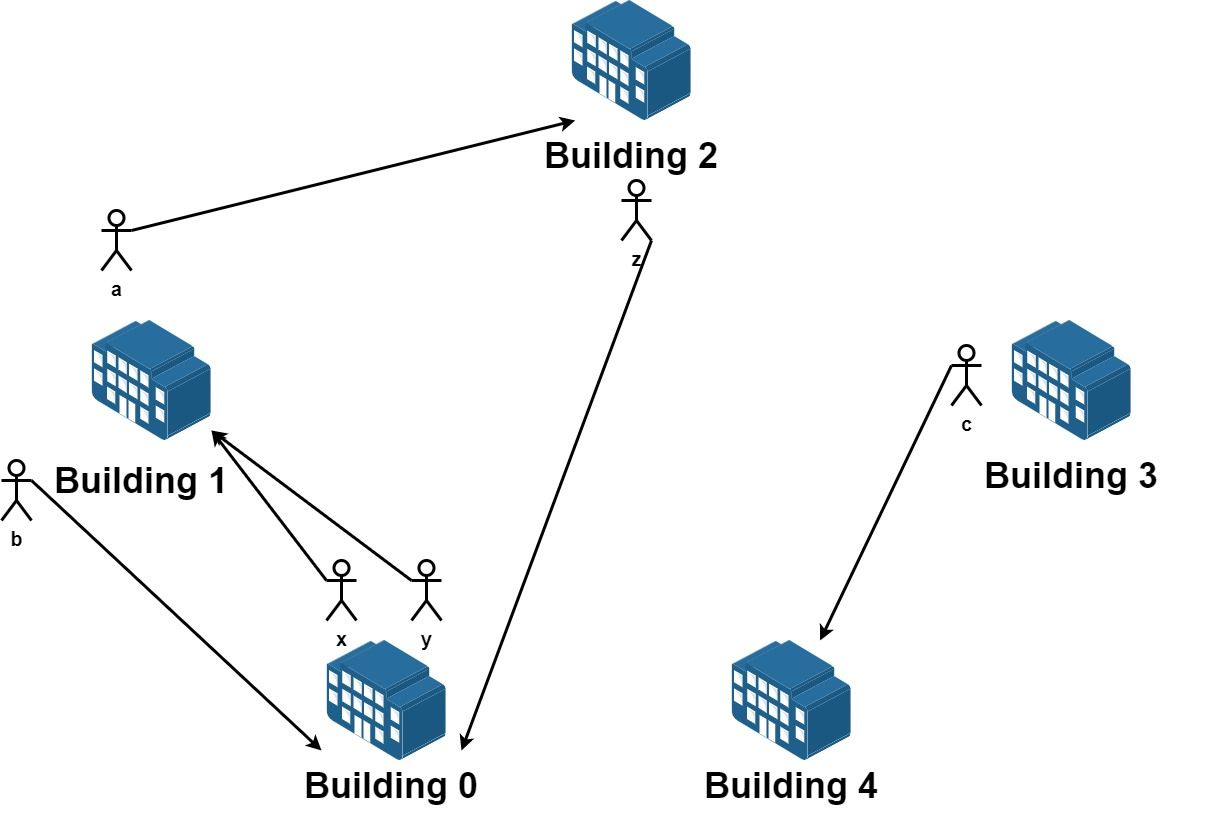
Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output: 5
Explantion: Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

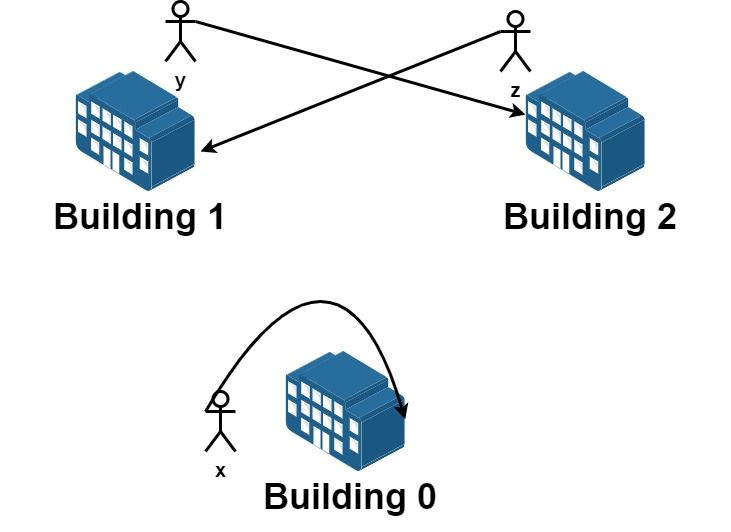
Input: n = 3, requests = [[0,0],[1,2],[2,1]]
Output: 3
Explantion: Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.

Example 3:

Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output: 4

Constraints:

1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= from_i, to_i < n

Solutions

class Solution {
    private int m;
    private int n;
    private int[][] requests;

    public int maximumRequests(int n, int[][] requests) {
        m = requests.length;
        this.n = n;
        this.requests = requests;
        int ans = 0;
        for (int mask = 0; mask < 1 << m; ++mask) {
            int cnt = Integer.bitCount(mask);
            if (ans < cnt && check(mask)) {
                ans = cnt;
            }
        }
        return ans;
    }

    private boolean check(int mask) {
        int[] cnt = new int[n];
        for (int i = 0; i < m; ++i) {
            if ((mask >> i & 1) == 1) {
                int f = requests[i][0], t = requests[i][1];
                --cnt[f];
                ++cnt[t];
            }
        }
        for (int v : cnt) {
            if (v != 0) {
                return false;
            }
        }
        return true;
    }
}

class Solution {
public:
    int maximumRequests(int n, vector<vector<int>>& requests) {
        int m = requests.size();
        int ans = 0;
        auto check = [&](int mask) -> bool {
            int cnt[n];
            memset(cnt, 0, sizeof(cnt));
            for (int i = 0; i < m; ++i) {
                if (mask >> i & 1) {
                    int f = requests[i][0], t = requests[i][1];
                    --cnt[f];
                    ++cnt[t];
                }
            }
            for (int v : cnt) {
                if (v) {
                    return false;
                }
            }
            return true;
        };
        for (int mask = 0; mask < 1 << m; ++mask) {
            int cnt = __builtin_popcount(mask);
            if (ans < cnt && check(mask)) {
                ans = cnt;
            }
        }
        return ans;
    }
};

class Solution:
    def maximumRequests(self, n: int, requests: List[List[int]]) -> int:
        def check(mask: int) -> bool:
            cnt = [0] * n
            for i, (f, t) in enumerate(requests):
                if mask >> i & 1:
                    cnt[f] -= 1
                    cnt[t] += 1
            return all(v == 0 for v in cnt)

        ans = 0
        for mask in range(1 << len(requests)):
            cnt = mask.bit_count()
            if ans < cnt and check(mask):
                ans = cnt
        return ans

func maximumRequests(n int, requests [][]int) (ans int) {
	m := len(requests)
	check := func(mask int) bool {
		cnt := make([]int, n)
		for i, r := range requests {
			if mask>>i&1 == 1 {
				f, t := r[0], r[1]
				cnt[f]--
				cnt[t]++
			}
		}
		for _, v := range cnt {
			if v != 0 {
				return false
			}
		}
		return true
	}
	for mask := 0; mask < 1<<m; mask++ {
		cnt := bits.OnesCount(uint(mask))
		if ans < cnt && check(mask) {
			ans = cnt
		}
	}
	return
}

function maximumRequests(n: number, requests: number[][]): number {
    const m = requests.length;
    let ans = 0;
    const check = (mask: number): boolean => {
        const cnt = new Array(n).fill(0);
        for (let i = 0; i < m; ++i) {
            if ((mask >> i) & 1) {
                const [f, t] = requests[i];
                --cnt[f];
                ++cnt[t];
            }
        }
        return cnt.every(v => v === 0);
    };
    for (let mask = 0; mask < 1 << m; ++mask) {
        const cnt = bitCount(mask);
        if (ans < cnt && check(mask)) {
            ans = cnt;
        }
    }
    return ans;
}

function bitCount(i: number): number {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

/**
 * @param {number} n
 * @param {number[][]} requests
 * @return {number}
 */
var maximumRequests = function (n, requests) {
    const m = requests.length;
    let ans = 0;
    const check = mask => {
        const cnt = new Array(n).fill(0);
        for (let i = 0; i < m; ++i) {
            if ((mask >> i) & 1) {
                const [f, t] = requests[i];
                --cnt[f];
                ++cnt[t];
            }
        }
        return cnt.every(v => v === 0);
    };
    for (let mask = 0; mask < 1 << m; ++mask) {
        const cnt = bitCount(mask);
        if (ans < cnt && check(mask)) {
            ans = cnt;
        }
    }
    return ans;
};

function bitCount(i) {
    i = i - ((i >>> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
    i = (i + (i >>> 4)) & 0x0f0f0f0f;
    i = i + (i >>> 8);
    i = i + (i >>> 16);
    return i & 0x3f;
}

public class Solution {
    private int m;
    private int n;
    private int[][] requests;

    public int MaximumRequests(int n, int[][] requests) {
        m = requests.Length;
        this.n = n;
        this.requests = requests;
        int ans = 0;
        for (int mask = 0; mask < (1 << m); ++mask) {
            int cnt = CountBits(mask);
            if (ans < cnt && Check(mask)) {
                ans = cnt;
            }
        }
        return ans;
    }

    private bool Check(int mask) {
        int[] cnt = new int[n];
        for (int i = 0; i < m; ++i) {
            if (((mask >> i) & 1) == 1) {
                int f = requests[i][0], t = requests[i][1];
                --cnt[f];
                ++cnt[t];
            }
        }
        foreach (int v in cnt) {
            if (v != 0) {
                return false;
            }
        }
        return true;
    }

    private int CountBits(int n) {
        int count = 0;
        while (n > 0) {
            n -= n & -n;
            ++count;
        }
        return count;
    }
}

1601 - Maximum Number of Achievable Transfer Requests

1601. Maximum Number of Achievable Transfer Requests

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1601. Maximum Number of Achievable Transfer Requests

Description

Solutions

All Problems

All Solutions