Formatted question description: https://leetcode.ca/all/1591.html

1591. Strange Printer II (Hard)

There is a strange printer with the following two special requirements:

On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
Once the printer has used a color for the above operation, the same color cannot be used again.

You are given a m x n matrix targetGrid, where targetGrid[row][col] is the color in the position (row, col) of the grid.

Return true if it is possible to print the matrix targetGrid, otherwise, return false.

Example 1:

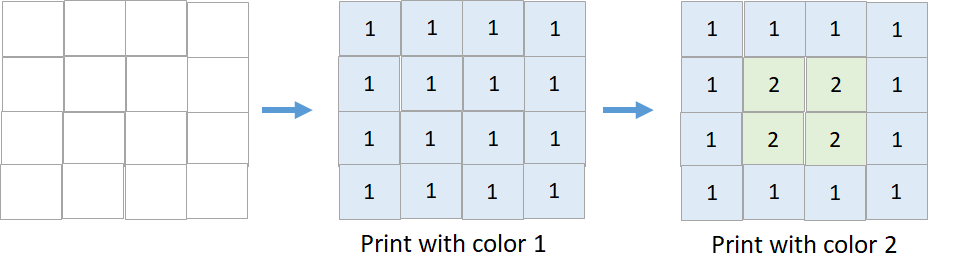
Input: targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
Output: true

Example 2:

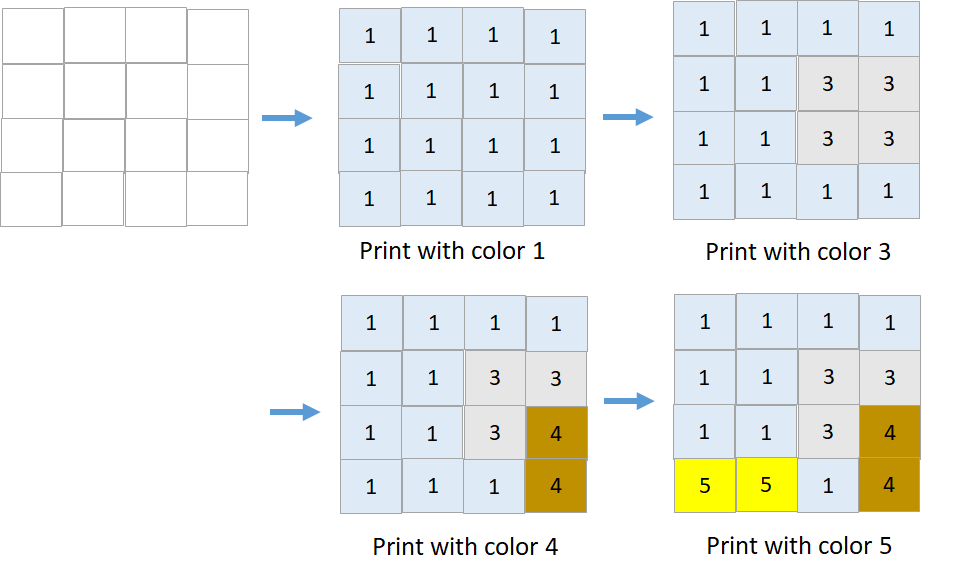
Input: targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
Output: true

Example 3:

Input: targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
Output: false
Explanation: It is impossible to form targetGrid because it is not allowed to print the same color in different turns.

Example 4:

Input: targetGrid = [[1,1,1],[3,1,3]]
Output: false

Constraints:

m == targetGrid.length
n == targetGrid[i].length
1 <= m, n <= 60
1 <= targetGrid[row][col] <= 60

Related Topics:
Greedy

Similar Questions:

Strange Printer (Hard)

Solution 1.

Java
C++

class Solution {
    public boolean isPrintable(int[][] targetGrid) {
        Map<Integer, int[]> boundsMap = new HashMap<Integer, int[]>();
        int rows = targetGrid.length, columns = targetGrid[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                int color = targetGrid[i][j];
                if (!boundsMap.containsKey(color))
                    boundsMap.put(color, new int[]{i, i, j, j});
                else {
                    int[] bounds = boundsMap.get(color);
                    bounds[0] = Math.min(bounds[0], i);
                    bounds[1] = Math.max(bounds[1], i);
                    bounds[2] = Math.min(bounds[2], j);
                    bounds[3] = Math.max(bounds[3], j);
                    boundsMap.put(color, bounds);
                }
            }
        }
        Set<Integer> keySet = boundsMap.keySet();
        Map<Integer, List<Integer>> greaterMap = new HashMap<Integer, List<Integer>>();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                int color = targetGrid[i][j];
                List<Integer> list = greaterMap.getOrDefault(color, new ArrayList<Integer>());
                for (int key : keySet) {
                    if (key != color) {
                        int[] bounds = boundsMap.get(key);
                        if (i >= bounds[0] && i <= bounds[1] && j >= bounds[2] && j <= bounds[3])
                            list.add(key);
                    }
                }
                greaterMap.put(color, list);
            }
        }
        Map<Integer, Integer> indegreeMap = new HashMap<Integer, Integer>();
        for (int color : keySet) {
            List<Integer> nextColors = greaterMap.getOrDefault(color, new ArrayList<Integer>());
            for (int nextColor : nextColors) {
                int indegree = indegreeMap.getOrDefault(nextColor, 0) + 1;
                indegreeMap.put(nextColor, indegree);
            }
        }
        Set<Integer> visited = new HashSet<Integer>();
        Queue<Integer> queue = new LinkedList<Integer>();
        for (int color : keySet) {
            int indegree = indegreeMap.getOrDefault(color, 0);
            if (indegree == 0) {
                visited.add(color);
                queue.offer(color);
            }
        }
        while (!queue.isEmpty()) {
            int color = queue.poll();
            List<Integer> nextColors = greaterMap.getOrDefault(color, new ArrayList<Integer>());
            for (int nextColor : nextColors) {
                int indegree = indegreeMap.getOrDefault(nextColor, 0) - 1;
                if (indegree == 0) {
                    indegreeMap.remove(nextColor);
                    visited.add(nextColor);
                    queue.offer(nextColor);
                } else
                    indegreeMap.put(nextColor, indegree);
            }
        }
        return visited.size() == keySet.size();
    }
}

// OJ: https://leetcode.com/problems/strange-printer-ii/
// Time: O(C^2 * MN)
// Space: O(MN)
class Solution {
    bool removable(vector<vector<int>> &G, vector<vector<int>> &pos, int c) {
        for (int i = pos[c][0]; i <= pos[c][2]; ++i) {
            for (int j = pos[c][1]; j <= pos[c][3]; ++j) {
                if (G[i][j] != c && G[i][j] != 0) return false;
            }
        }
        for (int i = pos[c][0]; i <= pos[c][2]; ++i) {
            for (int j = pos[c][1]; j <= pos[c][3]; ++j) G[i][j] = 0;
        }
        return true;
    }
public:
    bool isPrintable(vector<vector<int>>& G) {
        int M = G.size(), N = G[0].size();
        vector<vector<int>> pos(61, {M, N, 0, 0});
        unordered_set<int> colors, remove;
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                int c = G[i][j];
                colors.insert(c);
                pos[c][0] = min(pos[c][0], i);
                pos[c][1] = min(pos[c][1], j);
                pos[c][2] = max(pos[c][2], i);
                pos[c][3] = max(pos[c][3], j);
            }
        }
        while (colors.size()) {
            for (int c : colors) {
                if (removable(G, pos, c)) remove.insert(c);
            }
            if (remove.empty()) return false;
            for (int c : remove) colors.erase(c);
            remove.clear();
        }
        return true;
    }
};

1591 - Strange Printer II

1591. Strange Printer II (Hard)

Solution 1.

All Problems

All Solutions

Welcome to Subscribe On Youtube

1591. Strange Printer II (Hard)

Solution 1.

All Problems

All Solutions