Welcome to Subscribe On Youtube
1548. The Most Similar Path in a Graph
Description
We have n cities and m bi-directional roads where roads[i] = [ai, bi] connects city ai with city bi. Each city has a name consisting of exactly three upper-case English letters given in the string array names. Starting at any city x, you can reach any city y where y != x (i.e., the cities and the roads are forming an undirected connected graph).
You will be given a string array targetPath. You should find a path in the graph of the same length and with the minimum edit distance to targetPath.
You need to return the order of the nodes in the path with the minimum edit distance. The path should be of the same length of targetPath and should be valid (i.e., there should be a direct road between ans[i] and ans[i + 1]). If there are multiple answers return any one of them.
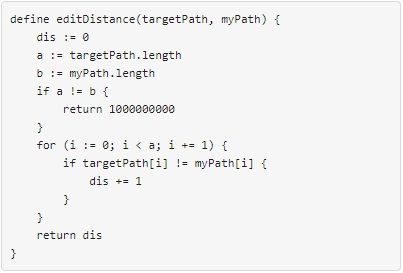
The edit distance is defined as follows:
Example 1:
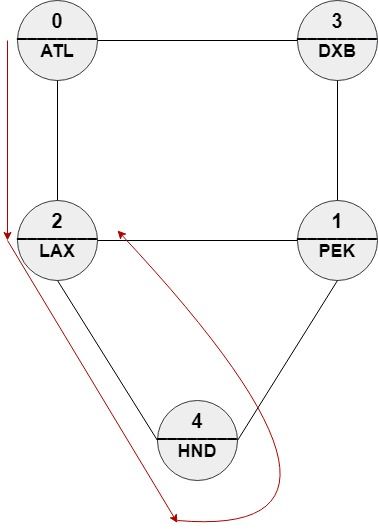
Input: n = 5, roads = [[0,2],[0,3],[1,2],[1,3],[1,4],[2,4]], names = ["ATL","PEK","LAX","DXB","HND"], targetPath = ["ATL","DXB","HND","LAX"] Output: [0,2,4,2] Explanation: [0,2,4,2], [0,3,0,2] and [0,3,1,2] are accepted answers. [0,2,4,2] is equivalent to ["ATL","LAX","HND","LAX"] which has edit distance = 1 with targetPath. [0,3,0,2] is equivalent to ["ATL","DXB","ATL","LAX"] which has edit distance = 1 with targetPath. [0,3,1,2] is equivalent to ["ATL","DXB","PEK","LAX"] which has edit distance = 1 with targetPath.
Example 2:
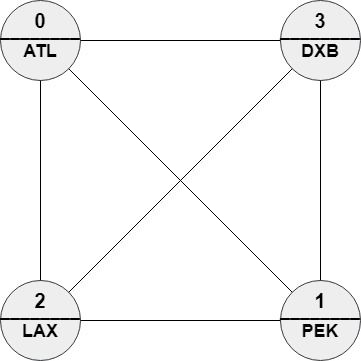
Input: n = 4, roads = [[1,0],[2,0],[3,0],[2,1],[3,1],[3,2]], names = ["ATL","PEK","LAX","DXB"], targetPath = ["ABC","DEF","GHI","JKL","MNO","PQR","STU","VWX"] Output: [0,1,0,1,0,1,0,1] Explanation: Any path in this graph has edit distance = 8 with targetPath.
Example 3:

Input: n = 6, roads = [[0,1],[1,2],[2,3],[3,4],[4,5]], names = ["ATL","PEK","LAX","ATL","DXB","HND"], targetPath = ["ATL","DXB","HND","DXB","ATL","LAX","PEK"] Output: [3,4,5,4,3,2,1] Explanation: [3,4,5,4,3,2,1] is the only path with edit distance = 0 with targetPath. It's equivalent to ["ATL","DXB","HND","DXB","ATL","LAX","PEK"]
Constraints:
2 <= n <= 100m == roads.lengthn - 1 <= m <= (n * (n - 1) / 2)0 <= ai, bi <= n - 1ai != bi- The graph is guaranteed to be connected and each pair of nodes may have at most one direct road.
names.length == nnames[i].length == 3names[i]consists of upper-case English letters.- There can be two cities with the same name.
1 <= targetPath.length <= 100targetPath[i].length == 3targetPath[i]consists of upper-case English letters.
Follow up: If each node can be visited only once in the path, What should you change in your solution?
Solutions
Solution 1: Dynamic Programming
We first build an adjacency list $g$ based on the given roads, where $g[i]$ represents the list of cities directly connected to city $i$.
Then we define $f[i][j]$ to be the minimum edit distance of the first $i$ cities of $targetPath$ and the first $j$ cities of $names$ when city $i$ of $targetPath$ matches city $j$ of $names$.
Then we can get the following recurrence equation:
\[f[i][j] = \min_{k \in g[j]} f[i - 1][k] + (targetPath[i] \neq names[j])\]In the process of state transition, we record the predecessor city of each state, and finally restore the optimal path from the end to the beginning according to the predecessor city array $pre$.
The time complexity is $O(m \times n^2)$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the lengths of $targetPath$ and $names$ respectively.
-
class Solution { public List<Integer> mostSimilar(int n, int[][] roads, String[] names, String[] targetPath) { List<Integer>[] g = new List[n]; Arrays.setAll(g, i -> new ArrayList<>()); for (int[] r : roads) { int a = r[0], b = r[1]; g[a].add(b); g[b].add(a); } int m = targetPath.length; final int inf = 1 << 30; int[][] f = new int[m][n]; int[][] pre = new int[m][n]; for (int i = 0; i < m; i++) { Arrays.fill(f[i], inf); Arrays.fill(pre[i], -1); } for (int j = 0; j < n; ++j) { f[0][j] = targetPath[0].equals(names[j]) ? 0 : 1; } for (int i = 1; i < m; ++i) { for (int j = 0; j < n; ++j) { for (int k : g[j]) { int t = f[i - 1][k] + (targetPath[i].equals(names[j]) ? 0 : 1); if (t < f[i][j]) { f[i][j] = t; pre[i][j] = k; } } } } int mi = inf, k = 0; for (int j = 0; j < n; ++j) { if (f[m - 1][j] < mi) { mi = f[m - 1][j]; k = j; } } List<Integer> ans = new ArrayList<>(); for (int i = m - 1; i >= 0; --i) { ans.add(k); k = pre[i][k]; } Collections.reverse(ans); return ans; } } -
class Solution { public: vector<int> mostSimilar(int n, vector<vector<int>>& roads, vector<string>& names, vector<string>& targetPath) { vector<int> g[n]; for (auto& r : roads) { int a = r[0], b = r[1]; g[a].push_back(b); g[b].push_back(a); } int m = targetPath.size(); int f[m][n]; int pre[m][n]; memset(f, 0x3f, sizeof(f)); memset(pre, -1, sizeof(pre)); for (int j = 0; j < n; ++j) { f[0][j] = targetPath[0] != names[j]; } for (int i = 1; i < m; ++i) { for (int j = 0; j < n; ++j) { for (int k : g[j]) { int t = f[i - 1][k] + (targetPath[i] != names[j]); if (t < f[i][j]) { f[i][j] = t; pre[i][j] = k; } } } } int k = 0; int mi = 1 << 30; for (int j = 0; j < n; ++j) { if (f[m - 1][j] < mi) { mi = f[m - 1][j]; k = j; } } vector<int> ans(m); for (int i = m - 1; ~i; --i) { ans[i] = k; k = pre[i][k]; } return ans; } }; -
class Solution: def mostSimilar( self, n: int, roads: List[List[int]], names: List[str], targetPath: List[str] ) -> List[int]: g = [[] for _ in range(n)] for a, b in roads: g[a].append(b) g[b].append(a) m = len(targetPath) f = [[inf] * n for _ in range(m)] pre = [[-1] * n for _ in range(m)] for j, s in enumerate(names): f[0][j] = targetPath[0] != s for i in range(1, m): for j in range(n): for k in g[j]: if (t := f[i - 1][k] + (targetPath[i] != names[j])) < f[i][j]: f[i][j] = t pre[i][j] = k k = 0 mi = inf for j in range(n): if f[-1][j] < mi: mi = f[-1][j] k = j ans = [0] * m for i in range(m - 1, -1, -1): ans[i] = k k = pre[i][k] return ans -
func mostSimilar(n int, roads [][]int, names []string, targetPath []string) []int { g := make([][]int, n) for _, r := range roads { a, b := r[0], r[1] g[a] = append(g[a], b) g[b] = append(g[b], a) } m := len(targetPath) const inf = 1 << 30 f := make([][]int, m) pre := make([][]int, m) for i := range f { f[i] = make([]int, n) pre[i] = make([]int, n) for j := range f[i] { f[i][j] = inf pre[i][j] = -1 } } for j, s := range names { if targetPath[0] != s { f[0][j] = 1 } else { f[0][j] = 0 } } for i := 1; i < m; i++ { for j := 0; j < n; j++ { for _, k := range g[j] { t := f[i-1][k] if targetPath[i] != names[j] { t++ } if t < f[i][j] { f[i][j] = t pre[i][j] = k } } } } mi, k := inf, 0 for j := 0; j < n; j++ { if f[m-1][j] < mi { mi = f[m-1][j] k = j } } ans := make([]int, m) for i := m - 1; i >= 0; i-- { ans[i] = k k = pre[i][k] } return ans } -
function mostSimilar( n: number, roads: number[][], names: string[], targetPath: string[], ): number[] { const g: number[][] = Array.from({ length: n }, () => []); for (const [a, b] of roads) { g[a].push(b); g[b].push(a); } const m = targetPath.length; const f = Array.from({ length: m }, () => Array.from({ length: n }, () => Infinity)); const pre: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => -1)); for (let j = 0; j < n; ++j) { f[0][j] = names[j] === targetPath[0] ? 0 : 1; } for (let i = 1; i < m; ++i) { for (let j = 0; j < n; ++j) { for (const k of g[j]) { const t = f[i - 1][k] + (names[j] === targetPath[i] ? 0 : 1); if (t < f[i][j]) { f[i][j] = t; pre[i][j] = k; } } } } let k = 0; let mi = Infinity; for (let j = 0; j < n; ++j) { if (f[m - 1][j] < mi) { mi = f[m - 1][j]; k = j; } } const ans: number[] = Array(m).fill(0); for (let i = m - 1; ~i; --i) { ans[i] = k; k = pre[i][k]; } return ans; }