Welcome to Subscribe On Youtube
1494. Parallel Courses II
Description
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.
In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semesters for the courses you are taking.
Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.
Example 1:
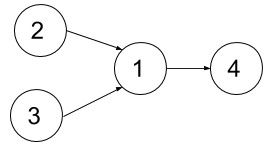
Input: n = 4, relations = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In the first semester, you can take courses 2 and 3. In the second semester, you can take course 1. In the third semester, you can take course 4.
Example 2:
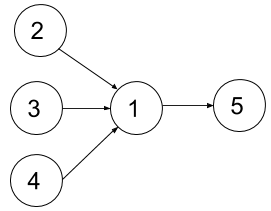
Input: n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In the first semester, you can only take courses 2 and 3 since you cannot take more than two per semester. In the second semester, you can take course 4. In the third semester, you can take course 1. In the fourth semester, you can take course 5.
Constraints:
1 <= n <= 151 <= k <= n0 <= relations.length <= n * (n-1) / 2relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique. - The given graph is a directed acyclic graph.
Solutions
Well this is a great problem to solve to understand the beauty of bitmask
First of all if you are thinking of making this AC by graph theory then you are wrong . This a NPC Problem (NP-complete problem) you cant solve it Polynomial time. There are some weak test in the problem thats it get AC even with graph theory approach . Basically you have to try every possible case for each day and each course.
How to do it?
Well we will use bitmask to solve this .
Now first of all we will need to take pre[i], that means pre[i] is a vector which will keep all the course that depend on ith course
for(int i=0;i<d.size();i++)
{
d[i][1]--;
d[i][0]--;
pre[d[i][0]].push_back(d[i][1]);
}
We decrease each node because that will help us in bitmasking as (1<<0)&m sets m’s 1st bit but (1«1)&m sets m’s 2nd bit
Now we will call a function that will solve it for use . As a parameter we will send how many courses are taken yet . Yes 0 courses are taken at the first
int minNumberOfSemesters(int N, vector<vector<int>>& d, int K) {
for(int i=0;i<d.size();i++)
{
d[i][1]--;
d[i][0]--;
pre[d[i][0]].push_back(d[i][1]);
}
return make(0);
Now the make function takes a parameter . we will call it mask (it is a integer) . Now does mask mean well if ith bit in the mask is 1 it means ith course is taken So if all the courses are taken then its done . Now if N=3 then (1«3) = 8(1000) and (1«3)-1 =7(111) So (1«n)-1 means all the n courses are taken . So if all the courses are taken then we need no more days to study
int make(int mask)
{
if(mask==(1<<n)-1)
return 0;
Now we will create an indegree vector . What does it stands for? Well indegree[i] means the number of course needs to be done before doing ith course
for(int i=0;i<n;i++)
{
if(mask&(1<<i)) // if this case is already taken . If you wonder but no course
continue; // is taken then wait its a recursion function , so in some
// call we may have took some course
for(int j=0;j<pre[i].size();j++) // increase indegree for all dependent course
{ // of i
indeg[pre[i][j]]++;
}
}
Now its easy to understand that the courses with 0 indegree and those who are not taken yet can be taken one this day . So we will create on more bitmask ok which will indicate the courses available . If the ith bit of ok is 1 then it means it can be taken on current day. int ok=0; // first of all no course can be taken
for(int i=0;i<n;i++)
{
if(indeg[i]==0&&!(mask&(1<<i))) // no dependency and not taken yet
{
ok|=(1<<i); // i guess you know or function
}
}
Now the number of set bit in ok is the number of course can be taken on this day. We can count the number of set by a builtin function __builtin_popcount(ok) . int available_course=__builtin_popcount(ok);
Great Now there can be 2 cases 1 where available_courses
So we will make all the subset mask of ok and try to solve for all remaining courses
for(int j=ok;j;j=(j-1)&ok)
{
int took=__builtin_popcount(j);
if(took!=k) // cant take or not optimal
continue;
else
{
taken=min(taken,1+make(mask|j)); // +1 is for using this day
} // mask|j make all course in j taken
}
Now what about available courses <= k Well then taking all of them is optimal
if(available_course>k)
{
for(int j=ok;j;j=(j-1)&ok)
{
int took=__builtin_popcount(j);
if(took!=k)
continue;
else
{
taken=min(taken,1+make(mask|j));
}
}
}
else
{
taken=min(taken,1+make(mask|ok));
}
We can initialize taken=n+1 as it wont be more than n+1 as answer
Now few more thing left like memoization So we can simply take a DP[(1«(n+1)] because setting all courses will take (1«n)-1 space we may declare indgeree vector each time in the function . Also make vector 2D for pre[19]
Ref: https://sohojeprogramming.blogspot.com/2020/07/1494-parallel-courses-ii.html
-
class Solution { public int minNumberOfSemesters(int n, int[][] relations, int k) { int[] d = new int[n + 1]; for (var e : relations) { d[e[1]] |= 1 << e[0]; } Deque<int[]> q = new ArrayDeque<>(); q.offer(new int[] {0, 0}); Set<Integer> vis = new HashSet<>(); vis.add(0); while (!q.isEmpty()) { var p = q.pollFirst(); int cur = p[0], t = p[1]; if (cur == (1 << (n + 1)) - 2) { return t; } int nxt = 0; for (int i = 1; i <= n; ++i) { if ((cur & d[i]) == d[i]) { nxt |= 1 << i; } } nxt ^= cur; if (Integer.bitCount(nxt) <= k) { if (vis.add(nxt | cur)) { q.offer(new int[] {nxt | cur, t + 1}); } } else { int x = nxt; while (nxt > 0) { if (Integer.bitCount(nxt) == k && vis.add(nxt | cur)) { q.offer(new int[] {nxt | cur, t + 1}); } nxt = (nxt - 1) & x; } } } return 0; } } -
class Solution { public: int minNumberOfSemesters(int n, vector<vector<int>>& relations, int k) { vector<int> d(n + 1); for (auto& e : relations) { d[e[1]] |= 1 << e[0]; } queue<pair<int, int>> q; q.push({0, 0}); unordered_set<int> vis{ {0} }; while (!q.empty()) { auto [cur, t] = q.front(); q.pop(); if (cur == (1 << (n + 1)) - 2) { return t; } int nxt = 0; for (int i = 1; i <= n; ++i) { if ((cur & d[i]) == d[i]) { nxt |= 1 << i; } } nxt ^= cur; if (__builtin_popcount(nxt) <= k) { if (!vis.count(nxt | cur)) { vis.insert(nxt | cur); q.push({nxt | cur, t + 1}); } } else { int x = nxt; while (nxt) { if (__builtin_popcount(nxt) == k && !vis.count(nxt | cur)) { vis.insert(nxt | cur); q.push({nxt | cur, t + 1}); } nxt = (nxt - 1) & x; } } } return 0; } }; -
class Solution: def minNumberOfSemesters(self, n: int, relations: List[List[int]], k: int) -> int: d = [0] * (n + 1) for x, y in relations: d[y] |= 1 << x q = deque([(0, 0)]) vis = {0} while q: cur, t = q.popleft() if cur == (1 << (n + 1)) - 2: return t nxt = 0 for i in range(1, n + 1): if (cur & d[i]) == d[i]: nxt |= 1 << i nxt ^= cur if nxt.bit_count() <= k: if (nxt | cur) not in vis: vis.add(nxt | cur) q.append((nxt | cur, t + 1)) else: x = nxt while nxt: if nxt.bit_count() == k and (nxt | cur) not in vis: vis.add(nxt | cur) q.append((nxt | cur, t + 1)) nxt = (nxt - 1) & x -
func minNumberOfSemesters(n int, relations [][]int, k int) int { d := make([]int, n+1) for _, e := range relations { d[e[1]] |= 1 << e[0] } type pair struct{ v, t int } q := []pair{pair{0, 0} } vis := map[int]bool{0: true} for len(q) > 0 { p := q[0] q = q[1:] cur, t := p.v, p.t if cur == (1<<(n+1))-2 { return t } nxt := 0 for i := 1; i <= n; i++ { if (cur & d[i]) == d[i] { nxt |= 1 << i } } nxt ^= cur if bits.OnesCount(uint(nxt)) <= k { if !vis[nxt|cur] { vis[nxt|cur] = true q = append(q, pair{nxt | cur, t + 1}) } } else { x := nxt for nxt > 0 { if bits.OnesCount(uint(nxt)) == k && !vis[nxt|cur] { vis[nxt|cur] = true q = append(q, pair{nxt | cur, t + 1}) } nxt = (nxt - 1) & x } } } return 0 }