1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Description

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [a_i, b_i, weight_i] represents a bidirectional and weighted edge between nodes a_i and b_i. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

Example 1:

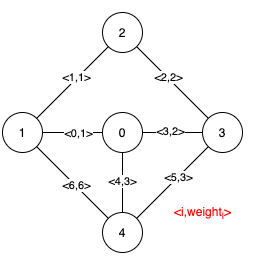
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

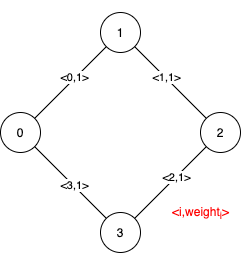
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

Constraints:

2 <= n <= 100
1 <= edges.length <= min(200, n * (n - 1) / 2)
edges[i].length == 3
0 <= a_i < b_i < n
1 <= weight_i <= 1000
All pairs (a_i, b_i) are distinct.

Solutions

class Solution {
    public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
        for (int i = 0; i < edges.length; ++i) {
            int[] e = edges[i];
            int[] t = new int[4];
            System.arraycopy(e, 0, t, 0, 3);
            t[3] = i;
            edges[i] = t;
        }
        Arrays.sort(edges, Comparator.comparingInt(a -> a[2]));
        int v = 0;
        UnionFind uf = new UnionFind(n);
        for (int[] e : edges) {
            int f = e[0], t = e[1], w = e[2];
            if (uf.union(f, t)) {
                v += w;
            }
        }
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < 2; ++i) {
            ans.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            int f = e[0], t = e[1], w = e[2], i = e[3];
            uf = new UnionFind(n);
            int k = 0;
            for (int[] ne : edges) {
                int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
                if (j != i && uf.union(x, y)) {
                    k += z;
                }
            }
            if (uf.getN() > 1 || (uf.getN() == 1 && k > v)) {
                ans.get(0).add(i);
                continue;
            }
            uf = new UnionFind(n);
            uf.union(f, t);
            k = w;
            for (int[] ne : edges) {
                int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
                if (j != i && uf.union(x, y)) {
                    k += z;
                }
            }
            if (k == v) {
                ans.get(1).add(i);
            }
        }
        return ans;
    }
}

class UnionFind {
    private int[] p;
    private int n;

    public UnionFind(int n) {
        p = new int[n];
        this.n = n;
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
    }

    public int getN() {
        return n;
    }

    public boolean union(int a, int b) {
        if (find(a) == find(b)) {
            return false;
        }
        p[find(a)] = find(b);
        --n;
        return true;
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

class UnionFind {
public:
    vector<int> p;
    int n;

    UnionFind(int _n)
        : n(_n)
        , p(_n) {
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        if (find(a) == find(b)) return false;
        p[find(a)] = find(b);
        --n;
        return true;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

class Solution {
public:
    vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
        for (int i = 0; i < edges.size(); ++i) edges[i].push_back(i);
        sort(edges.begin(), edges.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
        int v = 0;
        UnionFind uf(n);
        for (auto& e : edges) {
            int f = e[0], t = e[1], w = e[2];
            if (uf.unite(f, t)) v += w;
        }
        vector<vector<int>> ans(2);
        for (auto& e : edges) {
            int f = e[0], t = e[1], w = e[2], i = e[3];
            UnionFind ufa(n);
            int k = 0;
            for (auto& ne : edges) {
                int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
                if (j != i && ufa.unite(x, y)) k += z;
            }
            if (ufa.n > 1 || (ufa.n == 1 && k > v)) {
                ans[0].push_back(i);
                continue;
            }

            UnionFind ufb(n);
            ufb.unite(f, t);
            k = w;
            for (auto& ne : edges) {
                int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
                if (j != i && ufb.unite(x, y)) k += z;
            }
            if (k == v) ans[1].push_back(i);
        }
        return ans;
    }
};

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.n = n

    def union(self, a, b):
        if self.find(a) == self.find(b):
            return False
        self.p[self.find(a)] = self.find(b)
        self.n -= 1
        return True

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]


class Solution:
    def findCriticalAndPseudoCriticalEdges(
        self, n: int, edges: List[List[int]]
    ) -> List[List[int]]:
        for i, e in enumerate(edges):
            e.append(i)
        edges.sort(key=lambda x: x[2])
        uf = UnionFind(n)
        v = sum(w for f, t, w, _ in edges if uf.union(f, t))
        ans = [[], []]
        for f, t, w, i in edges:
            uf = UnionFind(n)
            k = sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
            if uf.n > 1 or (uf.n == 1 and k > v):
                ans[0].append(i)
                continue

            uf = UnionFind(n)
            uf.union(f, t)
            k = w + sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
            if k == v:
                ans[1].append(i)
        return ans

type unionFind struct {
	p []int
	n int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	return &unionFind{p, n}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	if uf.find(a) == uf.find(b) {
		return false
	}
	uf.p[uf.find(a)] = uf.find(b)
	uf.n--
	return true
}

func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int {
	for i := range edges {
		edges[i] = append(edges[i], i)
	}
	sort.Slice(edges, func(i, j int) bool {
		return edges[i][2] < edges[j][2]
	})
	v := 0
	uf := newUnionFind(n)
	for _, e := range edges {
		f, t, w := e[0], e[1], e[2]
		if uf.union(f, t) {
			v += w
		}
	}
	ans := make([][]int, 2)
	for _, e := range edges {
		f, t, w, i := e[0], e[1], e[2], e[3]
		uf = newUnionFind(n)
		k := 0
		for _, ne := range edges {
			x, y, z, j := ne[0], ne[1], ne[2], ne[3]
			if j != i && uf.union(x, y) {
				k += z
			}
		}
		if uf.n > 1 || (uf.n == 1 && k > v) {
			ans[0] = append(ans[0], i)
			continue
		}
		uf = newUnionFind(n)
		uf.union(f, t)
		k = w
		for _, ne := range edges {
			x, y, z, j := ne[0], ne[1], ne[2], ne[3]
			if j != i && uf.union(x, y) {
				k += z
			}
		}
		if k == v {
			ans[1] = append(ans[1], i)
		}
	}
	return ans
}

1489 - Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Description

Solutions

All Problems

All Solutions