Welcome to Subscribe On Youtube
1478. Allocate Mailboxes
Description
Given the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.
Return the minimum total distance between each house and its nearest mailbox.
The test cases are generated so that the answer fits in a 32-bit integer.
Example 1:
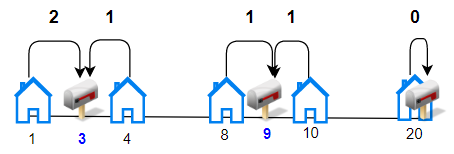
Input: houses = [1,4,8,10,20], k = 3 Output: 5 Explanation: Allocate mailboxes in position 3, 9 and 20. Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
Example 2:
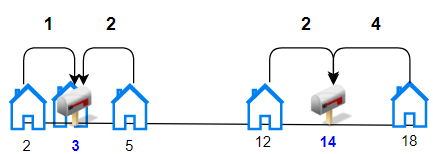
Input: houses = [2,3,5,12,18], k = 2 Output: 9 Explanation: Allocate mailboxes in position 3 and 14. Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
Constraints:
1 <= k <= houses.length <= 1001 <= houses[i] <= 104- All the integers of
housesare unique.
Solutions
-
class Solution { public int minDistance(int[] houses, int k) { Arrays.sort(houses); int n = houses.length; int[][] g = new int[n][n]; for (int i = n - 2; i >= 0; --i) { for (int j = i + 1; j < n; ++j) { g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i]; } } int[][] f = new int[n][k + 1]; final int inf = 1 << 30; for (int[] e : f) { Arrays.fill(e, inf); } for (int i = 0; i < n; ++i) { f[i][1] = g[0][i]; for (int j = 2; j <= k && j <= i + 1; ++j) { for (int p = 0; p < i; ++p) { f[i][j] = Math.min(f[i][j], f[p][j - 1] + g[p + 1][i]); } } } return f[n - 1][k]; } } -
class Solution { public: int minDistance(vector<int>& houses, int k) { int n = houses.size(); sort(houses.begin(), houses.end()); int g[n][n]; memset(g, 0, sizeof(g)); for (int i = n - 2; ~i; --i) { for (int j = i + 1; j < n; ++j) { g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i]; } } int f[n][k + 1]; memset(f, 0x3f, sizeof(f)); for (int i = 0; i < n; ++i) { f[i][1] = g[0][i]; for (int j = 1; j <= k && j <= i + 1; ++j) { for (int p = 0; p < i; ++p) { f[i][j] = min(f[i][j], f[p][j - 1] + g[p + 1][i]); } } } return f[n - 1][k]; } }; -
class Solution: def minDistance(self, houses: List[int], k: int) -> int: houses.sort() n = len(houses) g = [[0] * n for _ in range(n)] for i in range(n - 2, -1, -1): for j in range(i + 1, n): g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i] f = [[inf] * (k + 1) for _ in range(n)] for i in range(n): f[i][1] = g[0][i] for j in range(2, min(k + 1, i + 2)): for p in range(i): f[i][j] = min(f[i][j], f[p][j - 1] + g[p + 1][i]) return f[-1][k] -
func minDistance(houses []int, k int) int { sort.Ints(houses) n := len(houses) g := make([][]int, n) f := make([][]int, n) const inf = 1 << 30 for i := range g { g[i] = make([]int, n) f[i] = make([]int, k+1) for j := range f[i] { f[i][j] = inf } } for i := n - 2; i >= 0; i-- { for j := i + 1; j < n; j++ { g[i][j] = g[i+1][j-1] + houses[j] - houses[i] } } for i := 0; i < n; i++ { f[i][1] = g[0][i] for j := 2; j <= k && j <= i+1; j++ { for p := 0; p < i; p++ { f[i][j] = min(f[i][j], f[p][j-1]+g[p+1][i]) } } } return f[n-1][k] }