Welcome to Subscribe On Youtube
1463. Cherry Pickup II
Description
You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.
You have two robots that can collect cherries for you:
- Robot #1 is located at the top-left corner
(0, 0), and - Robot #2 is located at the top-right corner
(0, cols - 1).
Return the maximum number of cherries collection using both robots by following the rules below:
- From a cell
(i, j), robots can move to cell(i + 1, j - 1),(i + 1, j), or(i + 1, j + 1). - When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
- When both robots stay in the same cell, only one takes the cherries.
- Both robots cannot move outside of the grid at any moment.
- Both robots should reach the bottom row in
grid.
Example 1:
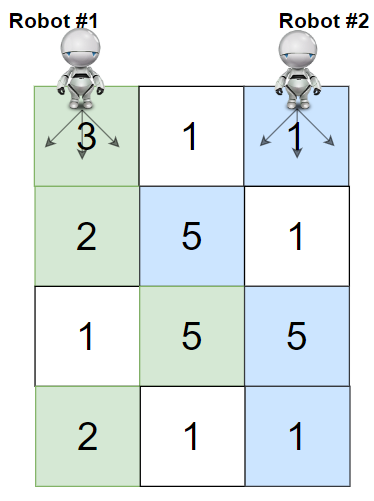
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]] Output: 24 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12. Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12. Total of cherries: 12 + 12 = 24.
Example 2:
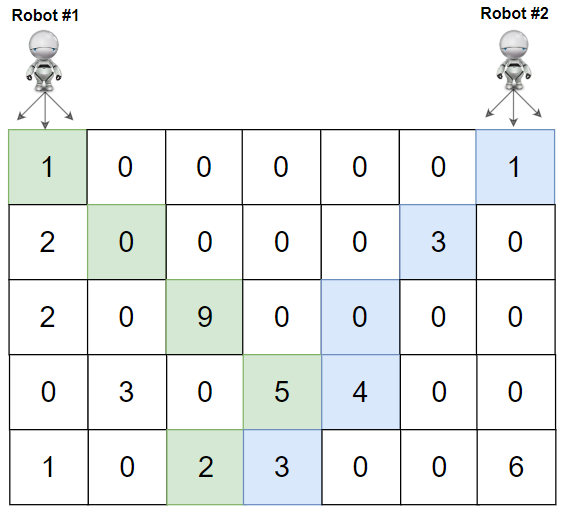
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]] Output: 28 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17. Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11. Total of cherries: 17 + 11 = 28.
Constraints:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
Solutions
Use dynammic programming, define dp[i][j1][j2]: The maximum cherries that both robots can take starting on the ith row, and column j1 and j2 of Robot 1 and 2 respectively.
-
class Solution { public int cherryPickup(int[][] grid) { int m = grid.length, n = grid[0].length; int[][][] f = new int[m][n][n]; for (var g : f) { for (var h : g) { Arrays.fill(h, -1); } } f[0][0][n - 1] = grid[0][0] + grid[0][n - 1]; for (int i = 1; i < m; ++i) { for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) { int x = grid[i][j1] + (j1 == j2 ? 0 : grid[i][j2]); for (int y1 = j1 - 1; y1 <= j1 + 1; ++y1) { for (int y2 = j2 - 1; y2 <= j2 + 1; ++y2) { if (y1 >= 0 && y1 < n && y2 >= 0 && y2 < n && f[i - 1][y1][y2] != -1) { f[i][j1][j2] = Math.max(f[i][j1][j2], f[i - 1][y1][y2] + x); } } } } } } int ans = 0; for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) { ans = Math.max(ans, f[m - 1][j1][j2]); } } return ans; } } -
class Solution { public: int cherryPickup(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); int f[m][n][n]; memset(f, -1, sizeof(f)); f[0][0][n - 1] = grid[0][0] + grid[0][n - 1]; for (int i = 1; i < m; ++i) { for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) { int x = grid[i][j1] + (j1 == j2 ? 0 : grid[i][j2]); for (int y1 = j1 - 1; y1 <= j1 + 1; ++y1) { for (int y2 = j2 - 1; y2 <= j2 + 1; ++y2) { if (y1 >= 0 && y1 < n && y2 >= 0 && y2 < n && f[i - 1][y1][y2] != -1) { f[i][j1][j2] = max(f[i][j1][j2], f[i - 1][y1][y2] + x); } } } } } } int ans = 0; for (int j1 = 0; j1 < n; ++j1) { for (int j2 = 0; j2 < n; ++j2) { ans = max(ans, f[m - 1][j1][j2]); } } return ans; } }; -
class Solution: def cherryPickup(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) f = [[[-1] * n for _ in range(n)] for _ in range(m)] f[0][0][n - 1] = grid[0][0] + grid[0][n - 1] for i in range(1, m): for j1 in range(n): for j2 in range(n): x = grid[i][j1] + (0 if j1 == j2 else grid[i][j2]) for y1 in range(j1 - 1, j1 + 2): for y2 in range(j2 - 1, j2 + 2): if 0 <= y1 < n and 0 <= y2 < n and f[i - 1][y1][y2] != -1: f[i][j1][j2] = max(f[i][j1][j2], f[i - 1][y1][y2] + x) return max(f[-1][j1][j2] for j1, j2 in product(range(n), range(n))) -
func cherryPickup(grid [][]int) int { m, n := len(grid), len(grid[0]) f := make([][][]int, m) for i := range f { f[i] = make([][]int, n) for j := range f[i] { f[i][j] = make([]int, n) for k := range f[i][j] { f[i][j][k] = -1 } } } f[0][0][n-1] = grid[0][0] + grid[0][n-1] for i := 1; i < m; i++ { for j1 := 0; j1 < n; j1++ { for j2 := 0; j2 < n; j2++ { x := grid[i][j1] if j1 != j2 { x += grid[i][j2] } for y1 := j1 - 1; y1 <= j1+1; y1++ { for y2 := j2 - 1; y2 <= j2+1; y2++ { if y1 >= 0 && y1 < n && y2 >= 0 && y2 < n && f[i-1][y1][y2] != -1 { f[i][j1][j2] = max(f[i][j1][j2], f[i-1][y1][y2]+x) } } } } } } ans := 0 for j1 := 0; j1 < n; j1++ { for j2 := 0; j2 < n; j2++ { ans = max(ans, f[m-1][j1][j2]) } } return ans } -
function cherryPickup(grid: number[][]): number { const m = grid.length; const n = grid[0].length; const f: number[][][] = new Array(m) .fill(0) .map(() => new Array(n).fill(0).map(() => new Array(n).fill(-1))); f[0][0][n - 1] = grid[0][0] + grid[0][n - 1]; for (let i = 1; i < m; ++i) { for (let j1 = 0; j1 < n; ++j1) { for (let j2 = 0; j2 < n; ++j2) { const x = grid[i][j1] + (j1 === j2 ? 0 : grid[i][j2]); for (let y1 = j1 - 1; y1 <= j1 + 1; ++y1) { for (let y2 = j2 - 1; y2 <= j2 + 1; ++y2) { if (y1 >= 0 && y1 < n && y2 >= 0 && y2 < n && f[i - 1][y1][y2] !== -1) { f[i][j1][j2] = Math.max(f[i][j1][j2], f[i - 1][y1][y2] + x); } } } } } } let ans = 0; for (let j1 = 0; j1 < n; ++j1) { for (let j2 = 0; j2 < n; ++j2) { ans = Math.max(ans, f[m - 1][j1][j2]); } } return ans; }